Слава Україні!
Адмін сайту, який є громадянином України та безвиїзно перебуває в Україні на протязі всього часу повномасштабної російської агресії, зичить щастя та мирного неба всім українським хлопцям та дівчатам! Також він рекомендує українським трейдерам кращих біржових та бінарних брокерів, що мають приємні торгові умови та не співпрацюють з російською федерацією. А саме:
Exness – для доступу до валютного ринку;
RoboForex – для роботи з CFD-контрактами на акції;
Deriv – для опціонної торгівлі.
Ну, і звичайно ж, заборонену в росії компанію Альпарі, через яку Ви маєте можливість долучитися як до валютного ринку, так і до торгівлі акціями та бінарними опціонами (Fix-Contracts). Крім того, Альпарі ще цікава своїми інвестиційними можливостями. Дивіться, наприклад:
рейтинг ПАММ-рахунків;
рейтинг ПАММ-портфелів.
Все буде Україна!
|
|
Для рядов с большим разбросом Лапедес предложил критерий средней относительной вариации:
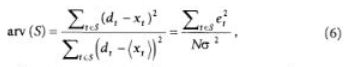
где S— временной ряд, е, — разность (истинное значение d, минус х,) в момент t, (х,) — оценка для среднего значения ряда, N — число данных в ряде. Последующая нормализация с помощью оценки для вариации позволяет проводить более надежные сравнения для различных приложений.
Используя предыдущее значение х, , целевой переменной, можно оценить способность модели предсказывать на один шаг вперед. Подставляя предсказанные значения на место истинных, получим метод предсказания на k шагов вперед. Если через несколько шагов модель начинает отклониться от настоящей траектории, это значит, что в ней происходит накопление и рост ошибки (см. [290], [275]).
Самый распространенный метод выбора нейронно-сетевой модели с наилучшим обобщением это проверка критерия согласия (MSE, ARV и др.) на тестовом множестве, которое не использовалось при обучении Если же данных мало, разбивать их на обучающее и подтверждающее множество нужно разными способами. Такое перекрестное подтверждение может потребовать много времени, особенно для нейронных сетей с их длительным процессом обучения.
В линейном анализе временных рядов можно получить несмещенную оценку способности к обобщению, исследуя результаты работы на обучающем множестве (MSE), число свободных параметров (W) и объем обучающего множества (N). Оценки такого типа называются информационными критериями (IC) и включают в себя компоненту, соответствующую критерию согласия, и компоненту штрафе, которая учитывает сложность модели. Барроном [30] были предложены следующие информационные критерии: нормализованный IC Акаикс (NAIC), нормализованный байесовский IC (NBIC) и итоговая ошибка прогноза (FPE):
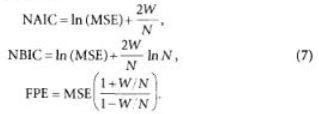
Было показано |198|, что FPE представляет собой несмещенную оценку способности к обобщению для нелинейных моделей, я частности, — для нейронных сетей. К сожалению, при этом предполагается, что в нашем распоряжении имеется бесконечное число на6людений, — в этом случае оценка надежности модели, вообще, не представляет особых сложностей.
Ясно, что информационные критерии дают информацию об адекватности модели и помогают выбрать модель подходящего уровня сложности. Другие методы диагностики позволяют, если такая задача стоит, избежать подхода к системе как к "черному ящику". Поскольку основное отличие сети от линейной регрессии — это возможность применять нелинейные преобразователи, имеет смысл посмотреть, насколько глубоко модель использует свои нелинейные возможности. Проще всего это сделать с помощью введенного Вигендом [275] отношения:
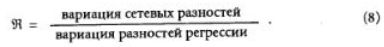
Для более тщательной проверки нелинейных возможностей нужно изобразить распределение выходных значений для скрытых элементов. Слишком большая доля крайних значений (0 или 1) говорит о том, что некоторые элементы попали в режим насыщения. Еще один способ — построить совместное распределение линейного и нелинейного выходов и применить линейную регрессию. Отклонения от наклона с углом 45е говорят о том, что нелинейные возможности задействованы [84;. Между прочим, встречается точка зрения, что появление во время обучения резких изменений разностей говорит об использовании нелинейностей. К сожалению, это не соответствуй действительности.
Следует также проверить, скоррелированны ли действия скрытых элементов. В многомерном регрессионном анализе при росте мультиколлинеарности значения коэффициентов регрессии становятся все менее надежными. Так же и здесь предпочтительно, чтобы выходы скрытых элементов одного слоя были некоррелированны. Нужно найти собственные значения корреляционной матрицы для выходов скрытых узлов по данным обработки всех обучающих примеров. При полной некоррелированности все собственные значения будут равны единице, а отличия от единицы говорят об избыточном числе скрытых элементов. Кроме того, для анализа внутреннего представления нейронно-сетевой модели часто применяются методы кластерного анализа.
Доводка
При построении системы прогноза преследуется цель не только расширить паше понимание процессов, но и получить помощь для принятия решений в финансовой области. Такого рода руководства можно создать с помощью комбинаций нескольких нейронных сетей, обученных на разных множествах данных и разных отрезках времени.
Например, сигналы на покупку или продажу будут даваться по пороговым значениям, которые настроены с учетом предыдущих позиций и ошибок. Очень важно также распознать момент, когда эффективность модели начинает падать.
|
