|
Терминология. Представляя терминологию, в рамках которой может быть описана «воля чистого случая», мы для полноты общей картины воспроизведем повторно некоторые из ранее данных определений.
«Чистая» случайность имеет место в пуассоновских процессах. Как ранее было определено, это означает невозможность для противоположных событий произойти одновременно, неизменность вероятности исходов в ходе испытаний и независимость вероятности исходов от истории. Кроме того, исходы испытаний должны отслеживаться при одинаковых исходных условиях.
«Дурная» неопределенность событий обусловлена «непуассоновскими свойствами» и неодинаковостью условий возникновения исходов.
Испытание — некоторый порядок действий, который может проводиться в виде опыта или эксперимента в целях получения некоторого исхода (например, бросок монеты и наблюдение сторон, которыми она выпадает; применение системы «чтения» поведения рынка и регистрация того, как срабатывает генерированный торговый сигнал).
Опыт — испытание, цель которого посмотреть, какой, вообще, может получиться результат-(исход).
Эксперимент ставится для проверки справедливости конкретной гипотезы в отношении того, какие конкретные исходы могут ожидаться.
Серия испытаний — повторение одного и того же испытания, проводимого определенное число раз.
Длина серии — число испытаний.
Игра — это серия испытаний различной длины, проводимых по определенным правилам, которые условно обозначают какие-то из возможных исходов как «успех» или «неудачу».
Событие (исход) — это результат мысленных или реальных испытаний. События различают по степени сложности: элементарные и составные.
Элементарные события — это такие, которые не разложимы ни на какие другие. Например, события «выпадение орла» и «выпадение решки» являются элементарными. Как и события «сигнал сработал» или «не сработал».
Составные события включают в себя какие-то другие, которые могут быть элементарными или более сложными по структуре (например, сразу несколько технических индексов «сигнализируют» об определенном состоянии рынка).
Произведение событий (логическое пересечение) означает их одновременность.
Сумма событий (логическое объединение) означает то, что события могут произойти либо по отдельности, либо одновременно.
Тогда, скажем, из двух любых событий X и Y можно составить, по крайней мере, два новых события с помощью таких логических операций, как:
1) пересечение (произведение событий) означает «одновременность X и Y» (связь через союз «и»). Пример: одновременно генерируется и сигнал — X, и его независимое подтверждение — Y;
2) объединение (сумма событий) означает, что имеют место «по отдельности или X, или Y либо одновременно и X, и Y» (обозначается союзом «и/или»). Пример: генерируется сигнал, который либо получает, либо не получает независимое подтверждение.
Как видим, объединение событий включает в себя их пересечение.
Совместимые события могут происходить одновременно (полностью или частично). Например, событие «сигнал сработал при первом испытании» совместимо с событием «сигнал не сработал при второй попытке применения». Могут произойти и то, и другое события.
Несовместимые события не могут произойти одновременно. Например, сигнал не может и сработать, и не сработать в одно и то же время, а монета — выпасть двумя сторонами сразу.
Пространство (поле) элементарных событий (ПЭС) — совокупность (множество) элементарных событий, которые представляют собой все мыслимые исходы испытаний. Это позволяет характеризовать каждый отдельный опыт (эксперимент) с точки зрения «объемности» того места, которое он занимает в ПЭС.
Важнейшее свойство ПЭС — вероятности всех его элементарных событий в сумме дают единицу (100%). Это означает, что при любом испытании хотя бы какое-то событие из этого поля обязательно произойдет.
ПЭС можно определить только тогда, когда точно определено содержание проводимого опыта или эксперимента.
Так, если испытание заключается всего в одном броске на удачу, то, согласно идеализированному представлению о монете, ПЭС состоит только из двух событий: «орел» и «решка». Вариант «ребро» не допускается.
Та же ситуация и при работе с сигналом: при каждом его применении он может оказаться либо истинным, либо ложным.
Изменение условий испытания меняет и ПЭС. Если, скажем, испытание заключается в том, чтобы бросить монету дважды, то пространство элементарных событий будет включать в себя уже четыре элементарных события: «орел-орел», «решка-решка», «орел-решка» и «решка-орел». Для г испытаний ПЭС будет содержать 2r событий.
Случайная величина (переменная) — некоторая функция, определенная на пространстве элементарных событий через исходы некоторого опыта или эксперимента.
Статистическая (безусловная) вероятность — численное значение, характеризующее меру неопределенности и возможности какого-то события или значения переменной величины.
Вероятность изменяется в пределах от 0 до 1:
• 0 — это оценка события как статистически определенного в качестве невозможного, сколько бы одинаковых испытаний не проводилось;
• 1 — оценка события как статистически определенного в качестве неизбежного, сколько бы одинаковых испытаний не проводилось;
• 0,5 означает статистическую неопределенность, когда при любом числе испытаний, скажем, имеющих только два исхода (событие есть или его нет), каждый раз следует в равной мере ожидать как свершения события, так и его отсутствия.
Условная вероятность — мера случайности события, которое рассматривается при условии одновременного совершения какого-то другого случайного события.
Шансы — это еще одна форма выражения вероятностной оценки, наиболее часто используемой при интуитивно-психологическом подходе, особенно там, где вероятности некоторого события X целесообразно «взвешивать» по дихотомии исходов «за» и «против».
Шансы, что некоторое событие X произойдет, принято выражать в форме:
a/b,
где а — любое число, характеризующее оценку «за» то, что событие X произойдет;
b — любое число, характеризующее оценку «против» того, что событие X произойдет.
Например, говорят, что шансы на успех в игре против рынка — 50:50.
Если известны величины а и b, то вероятность того, что событие X произойдет, вычисляется по формуле:
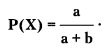
Можно видеть, например, что для события X, шансы которого оцениваются как 50:50, вероятность будет равна 0,5.
С другой стороны, если мы знаем значение вероятности Р(Х), то шансы в его пользу можно рассчитать по обратной формуле:
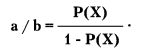
Иногда, в обыденной жизни оценки шансов и вероятности интересующего события ошибочно отождествляются. Так, если шансы на успех оцениваются как 1:10, то это вовсе не значит, что вероятность неудачи равна 0,1. Можно посчитать по формуле, приведенной выше, что на самом деле это 0,09.
Шансы — это не вероятность, а соотношение, так сказать, голосов «за» и «против». Поэтому вместо 50:50 можно в равной мере использовать 1:1 или 49:49. Существо оценки не изменится — соотношение «за» и «против» сохранится.
Комбинаторный анализ. Основные понятия комбинаторного анализа, которые нам необходимы, — это выборка и сочетание.
Представим совокупность каких-то двух видов элементов, случайно перемешанных в неизвестном соотношении. Это могут быть либо «орел» и «решка», либо сигнал «сработал» и «не сработал», либо «успех» и «неудача». Такая совокупность, которая может быть бесконечной по величине, называется генеральной.
Если последовательно r раз «запускать руку» в эту совокупность и случайным образом вытаскивать оттуда по одному элементу, то в результате получим какой-то набор «орлов» и «решек». Его и называют выборкой.
Примем, что порядковый номер результата выбора не имеет значения. Для нас важно соотношение возможных исходов: побед и поражений.
Тогда сделаем первое несложное вычисление: если «орлов» окажется к, то «решек» соответственно должно быть (r - k). Иначе говоря, при r попытках применения сигнала и к «успехах», будет соответственно r - k «неудач».
Очевидно, что оба эти элемента (исходы) могут располагаться в различных комбинациях. Например, «орел», «решка», «решка», «орел» и т.д. О каждом таком возможном варианте расположения к «орлов» и (r - k) «решек» принято говорить как о сочетании.
Из совокупности различных элементов можно делать случайные выборки, в которых имеющиеся элементы будут сочетаться тем или иным образом.
Количество комбинаций С(к/г), которыми к «орлов» могут сочетаться с (г - к) «решками», так просто уже не вычислишь. Для этого выведена следующая формула:
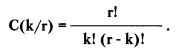
Например, для выборки r = 6 и при условии, что элементы «орел» и «решка» представлены по 3 каждый:
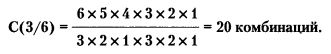
Это теоретически возможное количество сочетаний, какими складывается, например, равное число «успехов» и «неудач» в ряду из 6 операций трейдера.
В этой связи интересным для нас является вопрос: сколько всего мыслимых вариантов сочетаний элементов «успех» и «неудача» может возникнуть при r испытаниях? Для этого нужно вычислить и суммировать все виды сочетаний, где содержатся 0 «успехов» (r «неудач»), 1 «успех» (r -1 «неудача»), 2 «успеха» (r - 2 «неудачи») и т.д.
Например, для r = 2 получим:
С(0/2) + С(1/2) + С(2/2) = 1 + 2 + 1 = 4,
где С(0/2) — это число сочетаний, когда во всех r = 2 испытаниях не выпало ни одного «успеха» (одни лишь «неудачи»); С(1/2) — это число сочетаний, когда во всех r = 2 испытаниях выпал 1 «успех» и 1 «неудача»;
С(2/2) — это число сочетаний, когда во всех r = 2 испытаниях выпало 2 «успеха» (ни одной «неудачи»).
Для г = 3 будет другой результат:
С(0/3) + С(1/3) + С(2/3) + С(3/3) = 1+3 + 3 + 1 = 8,
где С(0/3) — это число сочетаний, когда во всех r = 3 испытаниях не выпало ни одного «успеха» (все «неудачи»);
С(1/3) — это число сочетаний, когда во всех r = 3 испытаниях выпал лишь 1 «успех» (а значит, остальные 2 были «неудачи»);
С(2/3) — это число сочетаний, когда во всех г = 3 испытаниях выпало 2 «успеха» (а значит, 1 «неудача»); С(3/3) — это число сочетаний, когда во всех г = 3 испытаниях выпадали только одни «успехи» (ни одной «неудачи»).
Это общий порядок расчета для любого числа возможных исходов в каждом отдельном испытании. Для частного случая, когда есть только два исхода («успех» и «неудача»), существует более простая формула (два в степени r):
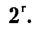
Тогда получаем те же результаты:
• при r = 2 число комбинаций равно два в степени два (4);
• при r = 3 число комбинаций равно два в степени три (8);
• при r = 4 число комбинаций равно два в степени четыре (16) и т.д.
Как видим, уже при 10 применениях одного и того же сигнала число вариантов цепочки из «успехов» и «неудач» превышает 1000 (точнее, 1024), а при 20 — выше миллиона (1 048 576). После 30 операций число сочетаний превышает миллиард. Это означает, что было бы крайне маловероятно найти двух игроков с одинаковой комбинацией результатов. Каждому трейдеру уготована своя уникальная история.
Безусловная вероятность. Оценка возможности некоторого события, осуществление которого не обусловлено возникновением каких-то других событий, называют безусловной вероятностью. Поскольку упоминание о «безусловности» принято опускать, в дальнейшем эту приставку мы будем использовать только в необходимых по смыслу случаях.
О безусловной вероятности говорят при оценке возможности события, наступление которого не зависит от осуществления каких-то других.
Обратим внимание на два основных правила расчета безусловной вероятности.
I. «Правило умножения»
Для любых двух независимых событий X и Y, которые определены на некотором ПЭС, вероятность того, что случится и то и другое, определяется по формуле:
P(X И Y) = P(X) X P(Y),
где Р(Х) и P(Y) — вероятности событий X и Y соответственно;
Р(Х и Y) — вероятность совместного осуществления обоих событий.
Данная формула носит название «правило умножения» вероятностей. Если событий не два, а больше, то их вероятности также перемножаются:
Р(Х и Y и ... и Z ) = Р(Х) х P(Y) ... х P(Z).
Пример независимых событий: два возможных исхода бросания монеты. События «выпал орел» и «выпала решка» не зависят одно от другого. Поэтому в сериях испытаний может попеременно происходить и то и другое в определенных пропорциях. Если монета «идеальная», то число событий будет примерно равным. Если центр тяжести у монеты «смещен» в какую-то сторону, то соотношение будет также меняться.
По этой причине приведенная формула используется для проверки независимости событий, данные о которых получены экспериментальным путем. Если выявляется нарушение равенства Р(Х и Y) = Р(Х) X P(Y), то это рассматривается как свидетельство некой взаимосвязи (корреляции) между событиями, которые ранее предварительно предполагались как независимые.
Наряду с взаимозависимостью или независимостью событий они также характеризуются и с точки зрения их совместимости.
Если независимые события несовместимы, то, естественно, справедливо:
Р(Х и Y) = Р(Х) х P(Y) = 0.
Такие события по испытаниям с монетой, как «выпал орел» и «выпала решка», являются не только независимыми, но и несовместимыми. В каждом отдельном испытании они не могут случиться одновременно. Произойдет только какое-то одно из них.
Тогда сказанное можно обобщить в следующей схеме:

II. «Правило сложения»
Для любых двух совместимых событий (зависимых или независимых) можно оценивать вероятность не их «произведения» (и одно, и другое), а «суммы» («логическое объединение»).
Этот вариант обозначается как имеет место «X или Y либо и X, и Y».
Если такие два взаимосвязанных или независимых события X и Y имеют вероятности соответственно Р(Х) и P(Y), а вероятность их совместного наступления — Р(Х и Y), то вероятность того, что имеет место одно или другое либо оба эти события одновременно, вычисляется по формуле:
Р(Х или Y либо X и Y) = Р(Х) + P(Y) - P(X и Y).
Если события несовместимы между собой, т.е. Р(Х и Y) = 0, тогда эта формула упрощается до
Р(Х или Y) = Р(Х) + P(Y).
Этот вариант и есть «правило сложения».
Если несовместимых событий больше двух, то их вероятности также складываются:
Р(Х или Y или ... или Z) = Р(Х) + P(Y) + ... + P(Z).
Для событий, которые являются совместимыми и независимыми, получаем:
Р(Х или Y) = Р(Х) + Р(Y) - Р(Х) х P(Y)= l-{l-P(X)}x{l-P(Y)}.
Эти положения можно представить следующей схемой:

На основе этих двух правил можно вести расчет вероятности произвольного события, определенного на некотором пространстве элементарных событий. Для этого используется следующая общая процедура:
1) определить ПЭС;
2) оценить вероятности элементарных событий;
3) вычислить долю интересующего события в общем ПЭС (по правилам пересечения и объединения).
Например, при броске «идеальной» монеты, когда оба исхода возможны в равной мере, ПЭС состоит из двух независимых и несовместимых событий: «орел» и «решка». Вероятность любого из них будет равна 1/2.
Рассмотрим расчет по этой модели для частного случая, когда шансы на то, что сигнал окажется «истинным» или «ложным», равны 50:50 (вероятность каждого исхода 1/2). Поинтересуемся, какова вероятность разных сочетаний «успеха» и «неудачи», если испытание будет состоять из 3 попыток.
Начнем с того, что построим пространство элементарных событий.
Оно будет содержать:
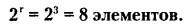
Это такие сочетания:
• «успех», «успех», «успех»;
• «успех», «успех», «неудача»;
• «успех», «неудача», «успех»;
• «неудача», «успех», «успех»;
• «успех», «неудача», «неудача»;
• «неудача», «успех», «неудача»;
• «неудача», «неудача», «успех»;
• «неудача», «неудача», «неудача».
Подчеркнем, что каждое из этих сочетаний является элементарным событием. Но напомним, что это верно только при испытании, которое определено как «три попытки применения сигнала».
Следующий шаг: оцениваем вероятности этих элементарных событий.
Согласно принятой модели случайности исхода «сработал — не сработал», нет причин, по которым одно сочетание, принадлежащее данному ПЭС, может быть вероятнее другого. Поэтому вероятность каждого из них приравнивается к одному и тому же значению 1/8 (всего восемь событий, и все равно возможны).
Теперь, наконец, можно приступать к оценкам вероятности любых интересующих сложных (составных) событий в рамках имеющегося перечня в ПЭС.
Для примера рассмотрим вероятность такого события: «имеет место хотя бы один успех».
Под это определение подходят варианты из ПЭС с любым числом успехов. Но не годятся те, где все три попытки — неудачные.
Тогда доля элементарных событий, попадающих под это определение, охватывает область из 7 элементов (все, кроме варианта «неудача», «неудача», «неудача»). В соответствии с этим вероятность интересующего события «имеет место хотя бы один успех» будет равна 7/8.
Можно посчитать, что такова же вероятность (7/8) и события: «имеет место хотя бы одна неудача».
Оба события («хотя бы один успех» и «хотя бы одна неудача») являются зависимыми и совместимыми.
Оценим вероятности «умножения» и «сложения» этих двух событий.
«Умножение» означает новое событие, которое определено как «хотя бы один успех и хотя бы одна неудача». На основе анализа ПЭС можно видеть, что этому условию в списке удовлетворяют 6 событий, т.е. все, за исключением первого (все успехи) и последнего (все неудачи). Тогда:
Р(Х и Y) = 6/8 = 3/4.
«Сложение» означает новое событие, которое определено так: «либо хотя бы один успех или неудача, либо и то и другое». На основе анализа ПЭС можно видеть, что этому условию в списке удовлетворяют все события, входящие в ПЭС, т.е. вероятность Р(Х или Y либо X и Y) = 1. Проверяем по соответствующей формуле:
Р(Х или Y либо X и Y) = 7/8 + 7/8 + 3/4 = 1.
Это означает: «что-нибудь да обязательно произойдет».
И еще пример, на котором мы здесь остановимся, поскольку он имеет значение для последующего рассмотрения.
Это оценка вероятности события: «имеет место, по крайней мере, два успеха подряд». Данное событие «охватывает» три элементарных события:
• «успех», «успех», «успех»;
• «успех», «успех», «неудача»;
• «неудача», «успех», «успех».
Тогда соответствующая вероятность равна 3/8.
Увеличим число «успехов» до максимума. Получим, что вероятность такого события («три успеха подряд») равна 1/8.
Если представить испытание как не три, а большее количество попыток, то легко видеть, что чем оно больше, тем еще более мизерной становится вероятность «безошибочности». Так, при 20 операциях она меньше одной миллионной.
В этой связи уместно было бы вновь обратить внимание на принципиальное отличие дополнительного измерения, где, согласно принятым допущениям, действует «чистый» случай, от «дурной» неопределенности традиционных пространств. Так, в поведении рынка нередко можно обнаружить несколько десятков отдельных движений подряд в одну и ту же сторону, что является крайне маловероятным событием. Поэтому и существуют оппоненты «теории случайного рынка».
Однако не найдется даже ничтожно малой горстки трейдеров, которые в дополнительном измерении эффективности системы своей работы имели, хотя бы изредка, пусть не десятки, а полдюжины успехов подряд. Данный факт мы рассматриваем как косвенное подтверждение достаточной приближенности к реалиям представления о случайности событий в дополнительном измерении.
Сопоставление вероятностных расчетов с эмпирическими данными об эффективности существующих систем принятия торговых решений косвенно подтверждают случайный характер дополнительного измерения.
Условная вероятность. Представим ПЭС как объединение двух непересекающихся (независимых) множеств событий X и Y.
Пусть событие Н — это множество, которое одновременно принадлежит и X, и Y. Иначе говоря, Н «пересекается» и с событием X, и с Y.
Тогда событие Н может быть представлено как сумма пересечений событий «X и Н» и «Y и Н» (см. рисунок).
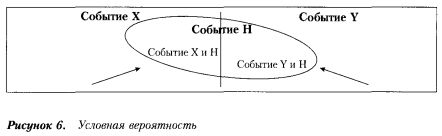
Далее, введем событие (Х/Н), которое следует читать: «X при условии свершения события Н». Соответственно событие (Y/H): «Y при условии свершения события Н».
Вероятность этих событий называют условной.
Условная вероятность — это оценка возможности наступления некоторого события при условии осуществления определенных других.
Проиллюстрировать ее определение можно на примере опыта: «выбор наугад фигуранта из некоего справочника действующих трейдеров», для каждого из которых там указаны также пол и опыт работы. Примем обозначения:
• событие X: «трейдер — женщина»;
• событие Y: «трейдер — мужчина»;
• событие Н: «трейдер с более чем 5-летним опытом работы».
Тогда событие Х/Н — это «случайно избранный фигурант оказался женщиной при условии, что попался опытный трейдер».
И событие Y/H — «случайно фигурант оказался мужчиной при условии, что попался опытный трейдер».
Очевидно, что выбор наугад может пасть на одну из четырех независимых категорий трейдеров: «женщина с опытом», «женщина-новичок», «мужчина с опытом» и «мужчина-новичок».
Поинтересуемся условной вероятностью события Р(Х/Н): «трейдер оказался женщиной при условии, что попался опытный трейдер» (т.е. событие «трейдер — женщина с опытом»).
По существу, задача состоит в том, чтобы вычислить долю женщин, обладающих нужным опытом работы, в общем объеме опытных трейдеров, числящихся в данном справочнике. В этом смысле все множество опытных трейдеров Н становится своего рода Новым Пространством Элементарных Событий (НПЭС).
Решение выражается формулой, которую принято рассматривать как исходное определение условной вероятности:
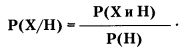
Здесь
Р(Х/Н) — условная вероятность интересующего события;
Р(Х и Н) — вероятность того, что женщина-трейдер окажется опытной;
Р(Н) — вероятность того, что при выборе попадется опытный трейдер (женщина или мужчина).
Как видно из рисунка:
Р(Н) = Р(Х и Н) + P(Y и Н).
Тогда вычисление вероятности можно проводить по другой формуле, которая известна как теорема Байеса. Она справедлива и для общего случая ряда независимых событий X, Y... Z:
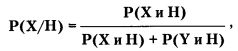
где Р(Х/Н) — вероятность события X при условии наступления события Н;
Р(Х и Н) — вероятность одновременного осуществления событий X и Н;
P(Y и Н) — вероятность одновременного осуществления событий Y и Н.
Если, например, события X и Н независимы (не пересекаются), то:
Р(ХиН) = Р(Х)хР(Н).
И тогда
Р(Х/Н) = Р(Х)
Р(Н/Х) = Р(Н).
Подчеркнем, что условная вероятность событий (Х/Н) или (Y/H) рассматривается не на всем первоначально обозначенном пространстве элементарных событий (X и Y), а лишь на той его части, которая ограничена множеством события Н. Поэтому термин «при условии» (Х/Н) не всегда означает «одновременно» (X и Н).
Дело в том, что именно множество Н, как уже отмечалось, становится новым пространством элементарных событий (НПЭС), которое входит составной частью в первоначальное ПЭС (X и Y).
В силу указанной причины событие Н называют также «приведенным пространством», являющимся «подпространством» ПЭС.
Вот почему в общем случае условная вероятность Р(Х/Н) отличается от Р(Х) и Р(Х и Н).
Эффект последействия. Важность понятия условной вероятности определяется наличием одного из главных допущений нашей модели «чистого» случая: независимость исхода каждого отдельного испытания от уже состоявшейся истории.
Смысл данного допущения — в отсутствии «эффекта последействия», что можно обнаружить именно через вычисление условной вероятности.
Рассмотрим для иллюстрации сказанного несколько опытов.
Опыт I: три последовательных броска монеты (применения заданного сигнала).
Определим следующее событие: «в третьей попытке выпадает успех» при условии, что «при первой попытке ждет неудача». Оценим его вероятность Р(успех = 3/неудача = 1). Формула расчета:
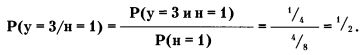
Выше мы уже построили ПЭС для данного опыта (8 элементарных событий). Получаем
Р(у = 3 и н = 1) = 1/4 (2 элементарных события из 8);
Р(н = 1) = 1/2 (4 элементарных события из 8).
Тогда
Р(у = 3/н = 1) = 1/4 : 1/2 = 1/2.
Действительно, приведенное пространство элементарных событий («неудача при первой попытке») состоит только из 4 элементов. А интересующее нас событие при этом условии («в третьей попытке удача») содержит только 2 элемента, что дает тот же результат:
Р(у = 3/н = 1) = 2:4 = У2.
Обратим внимание на то, что вероятность события «в третьей попытке выпадает успех при условии, что в первой ждет неудача» не означает произведения вероятностей событий «в третьей попытке успех» и «при первой попытке неудача».
Можно посчитать, что вероятность события «в третьей попытке успех при условии успеха и в первой» тоже будет равна У2.
Более того, если взять событие «в третьей попытке успех при условии успеха и в двух предыдущих», то окажется, что и тогда вероятность останется той же (У2).
Опыт II: проводится r последовательных испытаний (бросков монеты или применение сигнала).
Событие, вероятность которого требуется оценить: «в последней попытке выпадет успех (у) при условии, что во всех предыдущих была только неудача (н)».
Так, приведенное пространство элементарных событий содержит только 2 элемента: (н, н ... н, н) и (н, н ... н, у), где в каждом ряду по r исходов. Из этих двух элементарных и равновероятных событий есть одно, которое нас интересует (н, н .... н, у), что и дает неизменность шансов 50:50 при любом r.
С этим результатом трудно смириться психологически, но он наглядно демонстрирует ошибку «наивного здравого смысла». Неотвязным является ощущение, что чем больше случается повторений подряд одного и того же исхода, тем вероятнее становится нарушение этой «ненормальной» последовательности в очередной попытке. В попытке обосновать это ожидание на заре развития теории вероятности были даже написаны серьезные научные труды.
На самом деле вероятность нарушения одной и той же последовательности событий остается неизменной и равной 0,5. Она не зависит от истории предыдущих испытаний.
О данном явлении говорят как об отсутствии эффекта последействия.
Эффект последействия означает зависимость исходов текущих испытаний от истории тех, что уже состоялись. В пространствах случайных событий этот эффект отсутствует.
К сожалению, неверные в этом отношении интуитивные ощущения иногда могут стать обоснованием ложной игровой стратегии: ставка против какого-то, «слишком долго» продолжающегося тренда, в расчете на то, что он вот-вот изменится.
Надо сказать, что подобные ожидания, как правило, не оказываются обманутыми: в конце концов, тренд, и правда, меняется. Но вовсе не потому, как это думается, что «уже пора», а лишь тогда, когда того пожелает случай.
Подчеркнем, что учет отсутствия эффекта последействия имеет огромное значение для понимания некоторых выводов при анализе закономерностей случайных событий. И при последующем рассмотрении мы еще не раз будем обращаться к данному вопросу.
Удачливость. Suum cuique — каждому свое. Это и об удачливости тоже.
Под этим явлением принято понимать кажущееся присутствие в жизни человека неких неведомых сил, которые складывают для него обстоятельства, события и возможности во благо или во зло.
В дополнительном измерении действие этих сил проявляется как некая тенденция к возникновению повышенного числа «успешных» исходов в сравнении с математическим ожиданием в заданных условиях и на ограниченных участках испытаний.
Степень удачливости игрока проявляется в его индивидуальной предрасположенности к тому, что при прочих равных условиях исходы испытаний имеют тенденцию складываться более или менее «успешно».
Для дальнейших пояснений рассмотрим в качестве примера одну из моделей, которые в теории вероятностей называют «урновыми». С их помощью можно получить представление об одном важном эффекте, который связывают с удачливостью. Это так называемый эффект выбора. Проведем следующие опыты.
Опыт А: классический вариант с двумя урнами.
Имеются две урны с красными (а) и черными (в) шарами. Общее соотношение объемов этих урн n/m. В первой урне содержится a1 и b1 шаров, во второй — а2 и в2. Производится последовательная выемка шаров случайным образом с возвращением: вначале случайно определяется урна, а затем из нее «вслепую» вынимается шар, который после выяснения цвета возвращается обратно. Красные и черные шары везде одинаковы, но каждая из урн характеризуется собственным соотношением тех и других шаров.
Интересуемся условной вероятностью события: «если первый выбор пал на черный, то второй шар тоже окажется черным».
Эта схема рассматривается нами как модель следующей ситуации: имеется две группы (две урны) начинающих трейдеров, которые представлены в соотношении n : m (n < m).
Работе представителей первой урны (n «везунков») сопутствует «успех», который характеризуется тем, что на «прибыльные» операции (a1) у них приходится меньше «убыточных» (в1), т. е. a1 > в1.
Вторая группа — m «неудачников»: у них убыточных операций (в2) больше, чем прибыльных а2, т.е. а2 < в2.
Каждый из трейдеров в дилинговом зале может быть отнесен к одной из двух подгрупп, которые находятся в соотношении, — n и m. Но мы не знаем, кто есть кто, и ожидаем первого практического результата.
Конечно, случайностью будет то, у кого из трейдеров первая же операция завершится неудачей: это может случиться с представителем любой подгруппы. Однако, зарегистрировав данное событие, мы затем обращаем на этого трейдера особое внимание, задавшись правомерным вопросом: какова вероятность того, что следующий убыточный результат вновь будет принадлежать тому же фигуранту?
Это условная вероятность Р(рр/р), потому что она относится к событию, обусловленному совершенно определенными обстоятельствами: «если первый выбор пал на черный, то второй шар тоже окажется черным».
По известной формуле условной вероятности:
Р(вв/в) = Р(вв) / Р(в),
где Р(вв) — вероятность того, что черные шары окажутся при первой и второй выемках;
Р(в) — вероятность того, что при первой выемке окажется черный шар.
Можно найти, что:
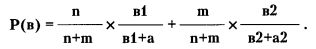
Тогда
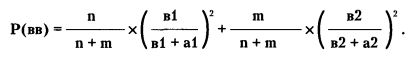
Для конкретного расчета допустим, что действует известная из практики обучения пропорция n : m = 1 : 9 (т.е. из 100 начинающих трейдеров 10 «везунков» и 90 «неудачников»). Допустим, что удачливость «везунков» выражается соотношением: на 3 успешных операции приходится 2 убыточных (60% успеха), а у неудачников это соотношение обратное —1:4 (20% успеха).
Получим
Р(в) = 0,76; Р(вв) = 0,59; Р(вв/в) = 0,59 : 0,76 = 0,78.
Таким образом, Р(вв/в) > Р(в). Это значит, что в сравнении с вероятностью неудачи в самый первый раз, когда трейдер начинал, так сказать, с «чистого листа», здесь можно видеть возрастание вероятности неудачи при условии провала предыдущей операции.
Не правда ли, возникает отчетливое ощущение, что налицо эффект последействия. Если это так, то мы приходим к противоречию данного расчета с исходным допущением о независимости исходов от истории.
Но можно на этот счет не беспокоиться: это ощущение — неверное.
Эффект выбора. Согласно объяснению В. Феллера, здесь наблюдается вовсе не эффект последействия. Вероятность исходов при независимых испытаниях все равно не связана с историей предыдущих опытов.
На самом деле имеет место эффект выбора, суть которого заключается в следующем.
Прежде всего, необходимо вновь подчеркнуть, что неудачливость (или удачливость) — это определенная предрасположенность, которая приводит к соответствующему результату. Он возникает вовсе не потому, что «это уже было» или «этого еще не было». Причина того или иного исхода — в повышенной вероятности данного события, что, в свою очередь, является следствием предрасположенности.
В силу того что «неудачники» более многочисленны, чем «везунки», а выбор делается случайным образом, то с повышенной вероятностью в поле нашего зрения «попадется на неудаче» именно трейдер из соответствующей группы. Но поскольку он имеет отрицательную предрасположенность к результатам (неудачливость), для него существует повышенные шансы и повторной неудачи. Как раз об этом и говорят более высокие значения условной вероятности.
Таким образом, условная вероятность оценивает в данном случае вовсе не эффект последействия, а возможность, так сказать, «повторной неудачи неудачника», который оказался нашим выбором.
Кто бы ни попался нам случайно в качестве объекта наблюдения («везунок» или «неудачник»), условная вероятность повторных событий будет отражать не его предыдущую историю, а предрасположенность к тем или иным исходам.
С какой предрасположенностью мы избрали объект наблюдения, такой результат, вероятнее всего, в последующем и получим.
В этом весь эффект выбора.
Эффект выбора заключается в том, что кто бы ни попался нам случайно в качестве объекта для повторного наблюдения, последующие события, вероятность которых оценивает условная вероятность, будут отражать предрасположенности объекта, а не его предыдущую историю.
Разумеется, неудача может приключиться и с трейдером-«везунком», который тем самым оказывается в поле нашего наблюдения. Но для него повторение неудачи — событие, хотя и возможное, но все же менее вероятное, чем для «неудачника».
Таким образом, хотя нужно признать связь истории с предрасположенностью (первая является определенным отражением второй), тем не менее, эффект последействия отличается от эффекта выбора. Это отличие выражается прежде всего в том, что при эффекте последействия история непосредственно влияет на будущий результат. А при действии эффекта выбора конкретный исторический результат не имеет значения, поскольку главную роль играет предрасположенность, склонность, тяготение к определенному исходу.
В известной мере аналогией здесь может служить сравнение технического и фундаментального анализа. Как известно, технический подход основан именно на анализе истории, из которой выводится представление о будущем. Фундаментальный же анализ делает упор на эффект работы экономических механизмов, которые проявляют себя не в «технической» зависимости от истории, но отражают глубинную «предрасположенность» сил спроса и предложения к подчинению определенным законам.
К слову сказать, именно на основании эффекта выбора страховые компании требуют увеличения взносов (страховых премий) со стороны тех, кто имеет склонность попадать в неприятности. Считается, что они, скорее всего, неудачники (в какой-то степени). Естественно, если с человеком «ничего такого» повторно не происходит, в оплату вносятся соответствующие изменения в лучшую сторону.
В практическом плане анализ эффекта выбора важен для понимания смысла неудач (или удач) как признака предрасположенности.
Если трейдера постигла неудача, то важнейший вопрос для понимания смысла этого события заключается в том, чтобы оценить, насколько здесь присутствует эффект выбора, а насколько — «чистая» случайность.
Иначе говоря, является ли полученный негативный результат показателем общей предрасположенности к неудачам («принадлежности» к отрицательной полуволне случайного блуждания), или все же имело место просто случайное отклонение в неблагоприятную сторону, а позже все образуется, и трейдеру вновь будет сопутствовать присущая ему удача?
В равной мере так же справедливо рассуждать и в ситуации, когда трейдер празднует удачу: этот успех является лишь единичным отклонением (откатом) от той сплошной цепи поражений, которая еще ждет впереди или, возможно, что все как раз наоборот, и эта удача не является случайным отклонением, а отражает предрасположенность к успеху и принадлежность трейдера к категории «везунков»?
Цепь неудачных (или успешных) операций должна анализироваться трейдером с точки зрения эффекта выбора. Он означает два варианта. Один: сложившийся результат является свидетельством принадлежности к группе «неудачников» (или «везунков»), и тогда это, вероятнее всего, будет иметь такое же продолжение. Другой вариант: имело место всего лишь случайное отклонение временного характера, и со временем все придет в «свою надлежащую норму».

Более определенный ответ на этот вопрос можно получить только по результатам более продолжительных последующих испытаний.
|

