|
Роль такой случайной величины в нашем рассмотрении играет показатель к (число «успехов»).
Практический интерес для нас при исследовании процесса случайного поведения эффективности, показатель которой выражается в значении к, представляют вопросы, которые связаны, прежде всего, со следующими характеристиками:
1) вероятность достижения суммарного «успеха» (величина к) вне зависимости от особенностей того или иного сочетания разных исходов, а также закономерные отклонения от ожидаемых величин;
2) вероятные конфигурации кривой эффективности, которые могут складываться по ходу испытаний.
Очевидно, что число «успехов» (k) может случайным образом изменяться в каждой серии r одних и тех же испытаний Бернулли в пределах от 0 до r.
При этом особенно важно отметить, что одному и тому же значению переменной k могут соответствовать разные конфигурации (профили) графика эффективности.
Число успехов в биномиальных испытаниях — это случайная величина. При этом одному и тому же значению к могут соответствовать графики различной конфигурации (профилей).
Наиболее вероятное значение. Каждое значение к, будучи случайной величиной, может характеризоваться своей вероятностью возникновения. Поэтому можно полагать, что в каждой модели существуют некие наиболее вероятные значения к. Слишком большие отклонения величины к от этих наиболее вероятных значений в какой-то конкретной серии испытаний менее вероятны, чем маленькие.
Следует подчеркнуть различие между вероятностью некого числа «успехов» Р(к) и вероятностью «успеха» р в каждом отдельном испытании.
Напомним, что важнейшей особенностью «чистого» случая является независимость вероятности «успеха» (р) в каждом отдельном испытании от истории предыдущих результатов. Соответственно вероятность «неудачи» q = 1 - р.
Нас интересуют вероятностные оценки Р(к/г/р) в зависимости от трех переменных:
• числа «успехов» к;
• исходных значений q и р в биномиальных испытаниях;
• длины серии r.
В рамках модели случайности можно рассматривать поведение кривой эффективности какого-то заданного «сигнала», имеющего определенную «оболочку» и конкретную «настройку» (по прибыли и убытку).
Одна из частных, но практически важных моделей — это «идеальная монета», где
p = q = 0,5.
Для модели «разновеликая монета» соотношение р : q может быть любым.
Как мы уже ранее видели, изменения априорных вероятностей р и q зависит от «настройки сигнала».
О способе теоретического расчета этих значений речь пойдет несколько позже. Что же касается эмпирических значений р и q, то их можно получить по результатам наблюдений числа «успехов» к в заданной серии испытаний r:
p = k/r (q = l - k/r),
где k — число «успехов» в г проведенных испытаниях.
Учтем, что число «неудач» будет равно (r - к). Соответственно суммарный баланс (число «успехов» минус число «неудач») можно представить в виде выражения:
k-(r-k) = 2k-r.
Допустим, что может быть проведено N серий по r испытаний в каждой. При этом результаты каждого испытания обозначим соответствующим «вектором эффективности» в дополнительном измерении, где:
• на оси абсцисс откладывается порядковый номер испытания (от 1 до r);
• на оси ординат — суммарный результат, т.е. текущая балансовая разница между абсолютными значениями «успехов» и «неудач».
Тогда результаты каждой серии испытаний предстанут на графике в виде кривой случайного блуждания длиной в r векторов. Проведя аналогию между r и временем Т, а также между балансовым результатом (2k - r) и пространством перемещения, можно говорить о пространственно-временном графике блуждания.
Если (2k - r) > 0, то точка блуждания находится в положительной части пространства (правая верхняя четверть). При (2k - r) < 0 точка находится в отрицательной половине (правая нижняя четверть).
Для каждой «нулевой отметки» (нахождение точки блуждания на оси абсцисс) справедливо равенство 2k = r.
Это означает, что число «успехов» и «неудач» будет равным при условии четности количества испытаний.
Рассмотрим событие: «r испытаний привели к суммарному числу успехов k (независимо от конфигурации их возникновения)».
В комбинаторике выведена формула расчета для общего случая р и q, и мы даем ее без вывода:
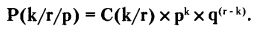
Для наглядности представим некоторые расчеты по испытаниям с «идеальной монетой», для которой р = q = 0,5.
Тогда можно рассчитать вероятность P(k/r/0,5) того, что r испытаний привели к раз к «успеху»:
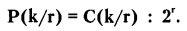
Случайная величина k имеет распределение результатов, которое называется биномиальным. Известно, что при постоянном значении r изменение этой функции в зависимости от k имеет примерно следующий вид (см. рисунок).
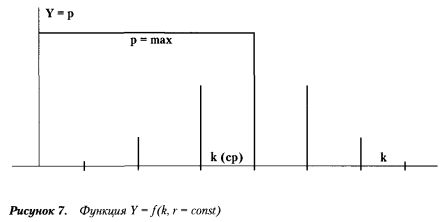
Как видим, максимальному значению вероятности соответствует определенное среднее число k(ср). Его называют наиболее вероятным числом «успехов».
Для условия р = q = 0,5 наиболее вероятное значение числа «успехов» k(ср) = r/2 (при четном значении r).
Каждое число «успехов» при биномиальных испытаниях имеет свою вероятность появления, зависящую от соотношения значений р и q. При р = q = 0,5 наиболее вероятное значение k(ср) = r/2.
Этот результат вполне соответствует обыденным представлениям.
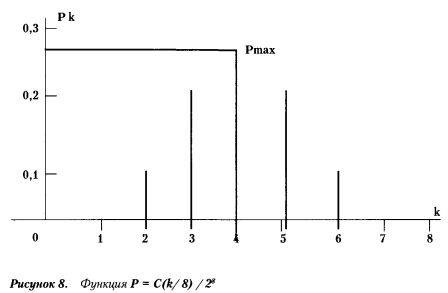
Можно рассчитать, что для испытаний, где r = 8 бросков монеты эта вероятностная функция будет принимать следующие значения:
Р( «успехов» = 0/r = 8) = 1: 256;
Р(1/8) = 8/256;
Р(2/8) = 28 / 256;
Р(3/8) = 56 / 256;
Р(4/8) = 70/256;
Р(5/8) = 56 / 256;
Р(6/8) = 28/256;
Р(7/8) = 8/256;
Р(8/8) = 1/256.
Как видим, наиболее вероятное число «успехов» равно 4. А конкретное значение вероятности этого события: 70 / 256 = 0,27 (см. рисунок).
Если r = 2k (четное число испытаний), то k(ср) = r/2. Так, если r = 100, наиболее вероятное число «успехов» — 50.
Математическое ожидание. Предварительно напомним, что выше были рассмотрены такие понятия, как:
• вероятности «успеха» (р) в каждом отдельном испытании;
• наиболее вероятное число «успехов» k(ср);
• вероятность определенного числа «успехов» Р(k/r/p).
Математическое ожидание числа «успехов» Е(k) является еще одним важным дополнительным понятием. Это среднее значение числа «успехов», которое, согласно математическим вычислениям, ожидается по результатам серии испытаний.
Математическое ожидание случайной величины — это синоним ее среднего значения, которое ожидается по результатам испытаний.
Подчеркнем, что в общем случае наиболее вероятное число «успехов» k(ср), которое определяется по максимальному значению вероятности определенного числа успехов P(k/r/p), отличается от математического ожидания числа успехов Е(к), хотя иногда может и совпадать.
Так, переменная величина числа «успехов» к может принимать значения от 1 до r. Каждому из них соответствует своя вероятность: Р(0), Р(1) ... Р(r). Тогда среднее значение числа «успехов», т.е. математическое ожидание по результатам г испытаний:
Е(k) = Р(0) х 0 + Р(1) х 1 + Р(2) х 2 + Р(3) х 3 + ... + Р(r) х r.
Как видим, каждое из возможных значений числа «успехов» оказывается, так сказать, «взвешенным» по вероятности своего возникновения.
Для интересующего нас биномиального распределения эта формула принимает вид:
E(k) = r x p.
При равновероятности исходов каждого испытания (р = q = 0,5):
E(k) = r x 0,5 = r / 2.
В данном примере математическое ожидание случайной величины k равно наиболее вероятному числу «успехов» k(ср). Но при неравенстве р и q такого совпадения может и не быть.
Предположим, что некая система генерирует сигнал, который характеризуется таким соотношением: р = 0,6 и q = 1 - р = 0,4. Пусть испытание заключается в двух применениях сигнала. Читатель может рассчитать самостоятельно, что наиболее вероятное значение числа «успехов» k(ср) = 1, при вероятности этого события Р(1) = 0,48. А математическое ожидание результата Е(k) = 1,2. Это означает, что, скажем, при 10 испытаниях (по два применения сигнала в каждом), т.е. всего 20 попыток, следует ожидать 12 «успехов». При 100 «двойных» испытаниях — 120 «успехов» и т.д.
Закон больших чисел. Его смысл прост: чем больше число испытаний, тем ближе число достигнутых «успехов» будет к его наиболее вероятному результату, выражением которого является математическое ожидание.
Для вышеприведенного примера (р = 0,6 и q = 0,4) чем больше испытаний сигнала, тем ближе среднее значение «успехов» к математически ожидаемой цифре 1,2.
Научная формулировка закона звучит более мудрено, но его смысл от этого не меняется. Для интересующей нас модели это звучит так:
• если проводить N серий при r испытаниях в каждой серии, то
среднее по сериям число достигаемых «успехов» к будет таково,
что величина {(k/r) - р} устремится к 0, как только N станет увеличиваться до бесконечности.
Иногда говорят иначе:
• с возрастанием N до бесконечности вероятность того, что доля
«успехов» k/r отклоняется от р на сколь угодно малую величину, стремится к нулю.
Согласно закону больших чисел, по мере возрастания числа испытаний уменьшается вероятность отклонений достигаемых результатов от их математического ожидания.
Как видим, закон говорит об ожидаемом конечном результате вполне определенно, т.е. звучит почти с детерминистической фатальностью. Ведь вероятность отклонений, равная нулю, — это достаточно определенная невозможность такого события.
Здесь мы подошли к моменту, имеющему ключевое значение для всего последующего рассмотрения, поскольку складывается впечатление, что закон больших чисел, как говорится, ставит «жирный крест» на надеждах иметь число «успехов», превышающее математическое ожидание.
Это и так, и не так.
Разумеется, этот закон незыблемо справедлив, и в бесконечном ряду испытаний результаты будут определенно равны математическому ожиданию.
Однако обратим внимание, что неотвратимость действия этого закона вступает в силу только по мере возрастания N.
К счастью, нерушимый закон больших чисел ничего не говорит о том, каково будет число «успехов» в каждой отдельной серии испытаний r, число которых ограничено. Здесь никакого долженствования, кроме вероятных оценок, еще не наступает.
На самом деле, если, например, зафиксировать продолжительность испытаний в каждой серии на уровне r, то значение числа «успехов» k от серии к серии будет случайным образом изменяться.
Закон больших чисел ничего не говорит о том, каким будет результат в каждой ограниченной серии испытаний. Долженствования здесь еще нет, только вероятность.
Дисперсия и стандартное отклонение. Возможный в ограниченных сериях испытаний разброс текущих результатов вокруг ожидаемого значения характеризуется с помощью таких понятий, как дисперсия и стандартное отклонение.
Для их понимания необходимо ввести другое важное определение: «квадратичное отклонение» случайной величины. Это квадрат разницы между средним значением k(ср) и тем, что наблюдается в конкретном эксперименте k, т.е. [(k(ср) - k]2.
Квадратичное отклонение - это квадрат разницы между ожиданием и реальным результатом.
Так, если k(ср) = 5, а в ходе какой-то серии испытаний было получено только 3 «успеха», то квадратичное отклонение будет равно:
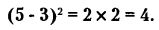
В других сериях квадратичные отклонения могут быть иными. Тогда можно рассчитать «среднее квадратичное отклонение»: просуммировать все квадратичные отклонения и разделить на число проведенных серий испытаний.
Это среднее квадратичное отклонение случайной величины обозначается как s2 и называется «дисперсией».
Дисперсия — это среднее квадратичное отклонение случайной величины от математического ожидания.
Если из дисперсии извлечь квадратный корень, то получим «стандартное отклонение» s.
Стандартное отклонение - это корень квадратный, извлеченный из дисперсии.
Теперь можно представить процедуру вычисления эмпирического значения дисперсии и стандартного отклонения.
Пусть, например, было проведено N серий испытаний с монетой, которые дали соответственно k0, k1, k2, k3 ... kr «успехов» в каждой. Тогда среднее число k(ср) по всем сериям:
кkср) = (k1, k2, k3 ... kr)/N.
Для вычисления дисперсии, или среднего квадратичного отклонения, s2 сумма квадратов отклонений от этого среднего складываются, и результат делится на N:
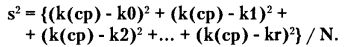
Стандартное отклонение, которое получается по экспериментальным данным, можно сравнивать с некими теоретическими значениями и на этом основании делать вывод, скажем, о соответствии монеты, примененной в эксперименте, «идеальной».
Для биномиального распределения формула принимает вид:
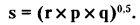
При р = q = 0,5 («идеальная» монета):
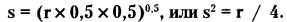
Для этой модели при серии, скажем, r = 100 испытаний стандартное отклонение s = 100 / 4 = 25. Поскольку наиболее вероятное число «успехов» k(ср) = 50, то можно ожидать, что колебание успешных испытаний от серии к серии будет происходить примерно в пределах между 25 и 75.
В этой связи возникает важный вопрос о том, насколько и как часто могут отклоняться экспериментальные результаты от тех, которые являются наиболее вероятными?
Для ответа на этот вопрос необходимо знать тот закономерный «профиль», каким распределяются случайные результаты в ходе испытаний при определенных исходных условиях.
Нормальное распределение. Это один из возможных «профилей» распределения случайной величины. Он характерен именно для биномиальной модели.
Для простоты изложения ограничимся только определениями.
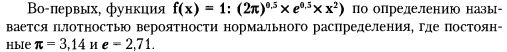
Эта функция показывает, каким образом изменяется вероятность события по мере его удаления от математического ожидания.
Нормальной функцией распределения, или распределением Гаусса, является интеграл этой функции, определенный для значений х от «минус бесконечности» до «х» (это означает — все возможные варианты удаления события от математического ожидания):
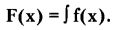
Можно убедиться, что «нормальным» в указанном математическом смысле является такой разброс результатов, при котором:
• 99,99% всех данных попадают в пределы 4 стандартных отклонений;
• 99,86% — в пределы трех стандартных отклонений;
• 97,72% — двух стандартных отклонений;
• 84,13% — одного стандартного отклонения.
Данный эталон (или стандарт) «нормальности» можно использовать при анализе экспериментально полученного распределения.
Нормальное распределение случайной величины характеризуется совершенно определенными «нормами» разбросов исходов результатов испытаний по отношению к математическому ожиданию.
Для нас важно то, что именно таким распределением отличаются пуассоновские случайные процессы.
В практическом плане интерес представляет оценка вероятности следующего события:
• число «успехов» в ходе биномиальных испытаний лежит в каких-то определенно заданных пределах.
Если такие пределы выражать в числе стандартных отклонений, то соответствующие оценки можно получить, воспользовавшись теоремой Чебышева.
Теорема (неравенство) Чебышева. В сравнении с распределением Гаусса эта теорема дает очень грубое приближение. Но зато она удобна в применении, поскольку позволяет сделать это быстро, не прибегая к обращению к сложным таблицам.
Согласно данной теореме, вероятность отклонения любой случайной величины k от среднего значения k(ср) в ту или иную сторону на расстоянии не более чем n раз по s (где n — положительное число) не меньше:
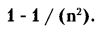
Диапазон отклонения значений к можно определить в виде неравенства:
{k(ср) - n х s) < k < (k(ср) + n х s).
Если задать n, то получим следующие оценки:
• для n = 3 (три стандартных отклонения в каждую сторону) с уве
ренностью не менее чем 89% следует ожидать, что все значения
случайной величины будут содержаться в пределах
(k(ср) - 3s) < k < (k(ср) + 3s);
• для n = 2 — с уверенностью не менее 75%, все значения случай
ной величины будут содержаться в пределах
(k(ср) - 2s) < k < (k(ср) + 2s);
• для n = 1 — нет никакой уверенности, что все значения случай
ной величины будут содержаться в пределах
(k(ср) - s) < k < (k(ср) + s).
Это позволяет соответствующим образом оценить получаемые экспериментальные результаты и увидеть, насколько они укладываются в схему «идеальной» монеты.
В нормальном распределении («чистая» случайность) чем больше число стандартных отклонений, тем меньше вероятность того, что результаты экспериментальных испытаний выйдут за установленные пределы.
При «чисто» случайных испытаниях чем больше взятое число стандартных отклонений, тем меньше вероятность выхода за эти пределы.
Вместе с тем, следует понимать вероятностно-статистический характер этой закономерности.

Она описывает не какую-то конкретную серию испытаний, а лишь указывает общую тенденцию, которая должна проявляться по итогам ряда экспериментов, повторяемых в одинаковых условиях.
|

