|
Временно представим себе, что мы не располагаем никакой информацией, кроме самих числовых данных. Обычно в таких случаях, начертив данные на графике, пытаются применить модель ARIMA, т.е. стараются найти закономерности типа авторегрессии или скользящего среднего. В табл. 3.4 представлены результаты анализа методом Бокса-Дженкинса для 5 лагов.
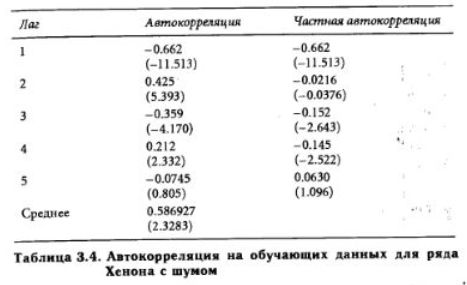
Поскольку после четырех лагов (за исключением 2-го) коэффициент автокорреляции и частной автокорреляции невелики, мы делаем вывод, что метод AR(4) подходит для этого ряда. Мы делаем прогноз для второй половины набора данных, исходя из четырех предыдущих значений х. Квадратный корень из среднеквадратичной ошибки (RMSE) прогноза равен 0.3642 .
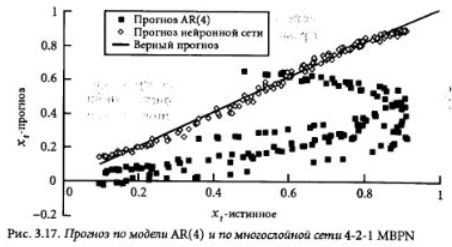
Этот же ряд мы проанализировали с помощью многослойной сети (MBPN). Зная вид модели, следовало бы взять сеть с двумя входами, но чтобы сохранить аналогию с четырьмя предыдущими значениями в методе Бокса-Дженкинса, мы выбрали архитектуру 4-2-1. Процесс обучения сели сходился не так хорошо, как в предыдущих двумерных примерах. При этом сходимость улучшалась, когда выбирались маленькие начальные значения весов (случайным образом на отрезке [-0.1,0.1]) и коэффициента обучения (0.1), Обучение прекращалось после 4000 эпох. В этот момент RMSE на пробном отрезке ряда (том же самом, что и в методе AR(4)) был равен 0.0649 и продолжал уменьшаться. Различие в точности прогноза сетью и линейной моделью оказалось здесь примерно таким же, как и в предыдущих экспериментах. Это хорошо видно на рис. 3.17. где результаты прогноза по обеим моделям сравниваются с точными значениями.
Как и следовало ожидать (учитывая, что ряд порожден моделью Хенона). прогноз по модели AR(4) имеет искажение параболическом формы. При внимательном изучении прогноза сети также можно заметить легкую синусоидальную волну вокруг истинных значений. Однако, амплитуда Искажения здесь во много раз меньше.
Взяв 1-мерный вход и не предполагая никаких знаний о модели, мы умышленно имели дело с сетью, содержащей лишние элементы. Как это обстоятельство повлияло на формирование весов в результате обучения сети? Для лучшего понимания вопроса в табл. 3.5 веса обученной сети представлены в сравнении с аналогичными весами двумерной сети (последние указаны в скобках). Веса входов, соответствующих t-1 и t-2, имеют для 4-лаговой и 2-лаговой моделей один и тот же знак и примерно одинаковую величину (по отношению к порогу)- Этот факт, а также малая среднеквадратичная ошибка прогноза 4-2-1 сети на новых образцах говорят об устойчивости характеристик сети при добавлении в нее лишних элементов.

Сравнение результатов прогноза
В заключение этой главы мы сравним качество прогноза, выдаваемого нелинейной нейронной сетью, с тем, что получается по метолу линейной регрессии, с помощью другой меры отклонения — 91. Эта мера была предложена Вигендом [275] и определяется как отношение остаточной дисперсии нелинейной модели к остаточной дисперсии линейной модели. Если две модели работают одинаково хорошо, это отношение равно 1. Малые значения & указывают на относительное превосходство нелинейной модели.

В эксперименте с временным рядом Хенона величина & была равна 0.12, что говорит о значительном превосходстве MBPN модели перед методом ARIMA. В последующих главах мы будем использовать отношение & для оценки прогнозов, касающихся реальных рыночных данных.
|

