НЕСКОЛЬКО НЕЙРОННО-СЕТЕВЫХ ЭКСПЕРИМЕНТОВ С ЛОГИСТИЧЕСКИМИ ВРЕМЕННЫМИ РЯДАМИ

Идет ли речь об эффективности рынка или о каких-либо других закономерностях, в любом случае выявить регулярное поведение во внешне случайной последовательности цен — очень интересная задача для любого аналитика. В примере временного ряда цен, показанном на рис 3.5, от исследователя потребуется определенная квалификация, чтобы суметь выделить совершенно четкую, хотя и скрытую, детерминированную закономерность. Савиту принадлежит замечание, что структуру хаотических систем легче понять, рассматривая их в более высоких размерностях. К сожалению, такое многомерное пространство может быть выбрано бесконечным числом способов.

Стандартный критерий Бокса-Дженкинса автокорреляции первого порядка предполагает линейность системы и не лает ключа к пониманию связей между р, , и р,, видимых на диаграмме. То же самое относится и к таким более сложным методам анализа временных рядов, как ARIMA. Самое большее, что можно будет получить, - это то, что очень высокие и очень низкие цены {и, соответственно, большие прибыли и потери) встречаются часто. Таким образом, распределение доходов будет иметь тяжелые хвосты и будет сильно отличаться от нормального. Статистические методы, которыми чаще всею пользуются экономисты, являются линейными и плохо отражают нелинейные динамические свойства саморегулирующихся рынков. Конечно, можно воспользоваться линейными методами с предварительным преобразованием, например, вместо какой-то из переменных взять ее логарифм или более высокую степень, но здесь возникают проблемы с выбором из слишком большого количества возможных преобразований. Кроме того, методы, основанные на средней квадратичной ошибке, плохо справляются с разрывами к траекториях хаотической модели.

Рассматривалась 1-2-1 MBPN-сеть (1 входной элемент, 1 скрытый слой из двух элементов и 1 выходной элемент), с полной связью между соседними слоями и бел прямых связей между входом и выходом. Сеть обучалась на последовательности входных значений р, , и выходных рг, полученных из соотношения (4). Мы использовали обобщенное нормальное обучающее правило дельта с коэффициентом обучения 0.9. Задача оказалась довольно простой. Для периода обучения было взято 3000 циклов, после чего мы предсказывали значения пены на 100 периодов вперед, а затем сравнивали их с "настоящими- значениями, вычисленными по формуле. Результаты представлены на рис. 3.7.

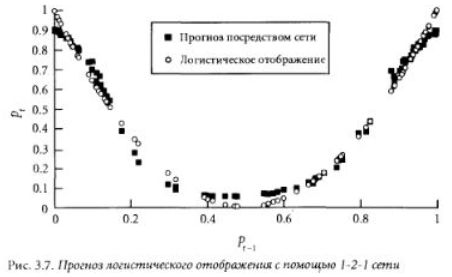
В области очень высоких и очень низких цен имеются некоторые отклонения, но в целом результаты выглядят вполне удовлетворительно.4 Корреляция между пеленой переменном и выходом сети составляет 0.9898, а среднеквадратичная ошибка прогноза равна 0.0026. При более длительном обучении и другом выборе параметров обучении можно добиться большей точности.

Вернемся теперь к первому варианту системы с квадратичной обратном связью (см. рис. 3.2) с параметрами с„ = 0-5, с, = -0.7, сг = 1.2, но теперь добавим к ней белый шум. Предположим, что изменения цены наполовину зависят от неинформированных инвесторов, которые реагируют на текущую цену в соответствии с приведенным выше соотношением, а на другую половину - от реакции информированных инвесторов на поступающую информацию о рынке, которая носит случайный характер. В нашей модели эта вторая составляющая мены брилась из нормального распределения с нулевым средним и стандартным отклонением 0.2. Результирующий доход есть среднее арифметическое от случайного дохода и дохода, определяемого обратной связью.

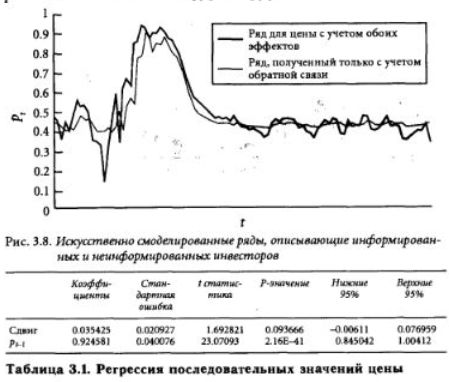
Жирной линией ни рис. 3.8 изображены цены с учетом всех видов дохода, а тонкой линией — цены, полученные на основе предсказанного дохода без учета вновь поступающей (случайной) информации Хорошо видно сглаживающее действие обратной связи: низкая цена дает сильную положительную обратную связь, а высокая — небольшую отрицательную. В табл. 3.1 приведены данные линейной регрессии между последовательными значениями цены р, , и р, для варианта с суммарными доходами. Поскольку сдвиг близок к нулю, а коэффициент для р, приблизительно равен единице, мы не можем отвергнуть гипотезу случайного блуждания, в соответствии с которой ожидаемое значение дни pf равно р,_,.

На рис. 3.9 представлена зависимость р, от р,, для ряда с полным учетом доходов. Как видно из рисунка, линия регрессии и квадратичная обратная связь вносят свой вклад в изменения цен. На этой точечной диаграмме трудно заметить нелинейную связь, потому что включенный во временной ряд случайный шум намного интенсивнее исходной детерминированной структуры.

Этот пример является хорошей проверкой способности нейронной сети выявлять исходную структуру. Здесь мы опять использовали полносвязную 1-2-1 сеть без непосредственных связей входа с выходом, которая обучалась с помощью входных значений р,, и целевых значений р,. Для обработки сетью многократно подавались наборы из 100 пар значений цен. Как и в первом эксперименте, коэффициент обучения был взят равным 0.9. Во время обучения сети по окончании очередной эпохи (т.е. каждые 100 циклов) вычислялась среднеквадратичная ошибка (MSE). С самого начала этот показатель плавно уменьшался с каждой новой эпохой. Мы продолжали обучение до тех пор, пока MSE не установилась на своем минимальном значении. Это произошло примерно через 4000 эпох. Затем с помощью обученной сети мы сделали прогноз величины р, по 100 новым тестовым значениям р,_,. Результаты представлены на рис. 3.10.

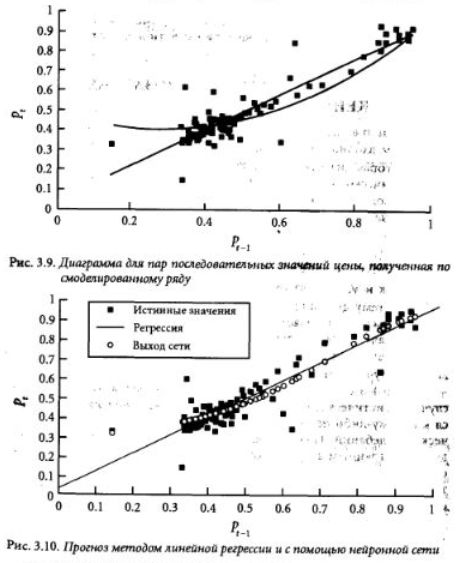
Наиболее критическим является участок относительно низких цен, где механизм обратной связи наиболее силен. На диаграмме в числе прочего показаны выход нейронной сети и прогноз по регрессии для таких критических значений р1Л. Очевидно, что сеть вполне удовлетворительно распознает исходную нелинейную взаимосвязь Интересно при этом, что RMSE (квадратный корень из средней квадратичной ошибки) прогноза нейронной сети (0.0635) всего на 5% лучше, чем у регрессии. Основной вклад в это улучшение вносит именно повышенная точность в области низких цен, где наиболее силен эффект обратной связи.

Содержание

Далее

На финансовых рынках время от времени случаются неожиданные события, например, девальвации валют, и здесь кроются наибольшие возможности для извлечения прибили.