|
Во-первых, это те, что получены как итог применения определенной системы «чтения» поведения рынка непосредственно по данным из традиционных измерений.
Во-вторых, это результаты, которые возникают на другом уровне рассмотрения: при использовании систем «чтения» данных, но не в традиционных, а в дополнительных измерениях разного порядка производности.
Результаты эффективности применения разных систем «чтения» поведения рынка могут оцениваться как на уровне традиционных пространств, так и дополнительных измерений разного уровня производности.
В соответствии с этим могут возникать и разные последовательности этапов принятия решений.
Для их рассмотрения введем понятие уровня оценки результата.
Тогда первый такой уровень — это оценка результатов работы в дополнительном измерении нулевого порядка производности (см. рисунок).
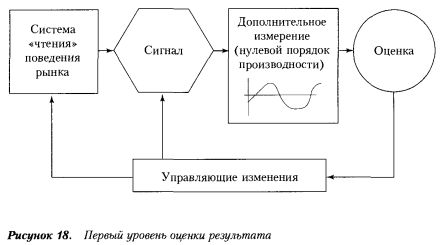
На втором уровне оценки результатов добавляется еще одно звено. Это дополнительное измерение первого порядка производности (см. рисунок).

Точка финансовой безубыточности. Это наиболее важный параметр, относительно которого производится оценка текущего результата на любом уровне рассмотрения.
Точка безубыточности в дополнительном измерении — это точка, в которой результаты работы с некоторым сигналом оказываются «нулевыми».
В дополнительном измерении «нулевой результат» может рассчитываться по двум параметрам:
• числу «успехов» и «неудач»;
• количеству «пунктов прибыли» и «пунктов убытка».
Точка безубыточности в дополнительном измерении может быть рассчитана как по соотношению числа успехов и неудач в применении сигнала, так и по балансу полученных (или проигранных) базисных пунктов.
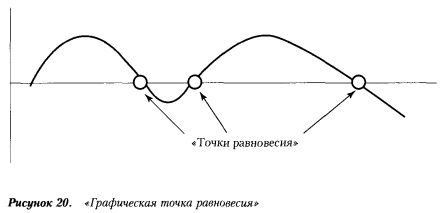
В соответствии с этим можно ввести понятие «графическая точка равновесия работы сигнала». Это порядковый номер «сигнала» (ось абсцисс), при котором достигается равенство числа «успехов» и «неудач».
Графически это выглядит как точка, где кривая изменения эффективности пересекает ось абсцисс (см. рисунок).
Графическая точка равновесия лежит на пересечении кривой эффективности с осью абсцисс.
Данный показатель важен при оценке действенности корректив, которые вносятся в «настройку» заданного сигнала.
Точка финансовой безубыточности означает «нулевой» финансовый результат (убыток равен прибыли), исчисленный, например, в базисных пунктах.
Понятно, что в зависимости от преимущественного сдвига «настройки» сигнала в сторону ожидаемой прибыли или допустимого убытка графическая точка равновесия может означать противоположные финансовые результаты. Так, если величина stop-profit будет больше stop-loss, то «точка равновесия» означает финансовую прибыль, а при обратном соотношении — убыток.
Таким образом, в графическом изображении точка безубыточности может находиться не только на пересечении кривой с осью абсцисс, но выше или ниже ее.
Положение «точки финансовой безубыточности» зависит от соотношения стоп-ордеров и поэтому может находиться в любом месте дополнительного измерения.
Для каждой точки финансовой безубыточности справедливо равенство:
k x SP = (r - k) x SL,
где r — общее число проведенных операций («безубыточных»);
к — число «успешных» операций;
(r - k) — число «неудачных» операций;
SP — «настройка сигнала» (в базисных пунктах) по стоп-ордеру на ожидаемую прибыль;
SL — «настройка сигнала» (в базисных пунктах) по стоп-ордеру на предельно допустимый убыток.
В практическом плане важно знать, сколько необходимо провести успешных операций из общего числа, чтобы обеспечить «финансовую безубыточность». Для этого данную формулу можно записать иначе:
r = kx(l + SP/SL).
Тогда, например, при SP = SL получим, что r = 2k. Это значит, что количество успешных операций, при котором наступает «финансовая безубыточность», всегда равно половине их общего числа. Очевидно, что оно должно быть четным.
Возьмем другое соотношение стоп-ордеров:
• SP = 60 базисных пунктов;
• SL = 30 базисных пунктов.
Из формулы можно найти, что «финансовая безубыточность» будет наступать каждый раз, когда r = k х (1 + 60/30) = 3k.
Если в качестве «единицы измерения» взять одну успешную операцию (к = 1), то число операций, завершившихся «безубыточно», будет r = 3, из которых две убыточные и одна успешная.
Таким же образом можно сделать расчеты и по другим соотношениям стоп-ордеров.
Выделим, прежде всего, два аспекта оценки текущего результата относительно финансовой точки безубыточности:
• фактическая степень благоприятной или неблагоприятной удаленности;
• тенденция к улучшению или ухудшению ситуации.
Текущие результаты работы могут оцениваться в дополнительных измерениях разного порядка производности по удаленности от точки «финансовой безубыточности» и тенденциям к улучшению или ухудшению складывающейся ситуации.
В зависимости от этого могут быть использованы разные рычаги управления по результатам. Например, «перенастройка» сигнала или объявления «стоп-операция» либо вообще смена всей системы «чтения» поведения рынка (см. рисунок).
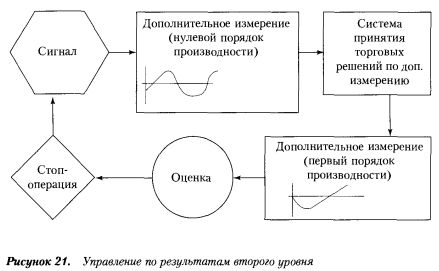
Движущаяся вероятность. Как уже говорилось, исход применения сигнала в каждом отдельном случае может быть оценен с точки зрения некоторой вероятности:
успеха (р);
неудачи (q = 1 - р).
Такая оценка может быть проведена применительно к дополнительному измерению любого порядка производности. При этом в качестве основы для расчетов могут служить как статистические данные предыдущих испытаний, так и некие теоретические положения, позволяющие делать выводы аналитическим путем.
Параметр вероятности исхода, означающий оценку ожидания успеха или неудачи, может рассчитываться экспериментально или аналитически в дополнительных измерениях любого порядка производности.
Движущаяся вероятность (ДВ) определяется как некий аналог движущихся средних, т.е. это доля числа «успехов» (к) в каком-то заранее заданном и зафиксированном количестве испытаний (с), которое «двигается» по всему отрезку r:
ДВ = к/с.
Естественно, что значение переменной с должно быть меньше общего число испытаний r (т.е. с < r). Тогда есть, так сказать, пространство для движения. Понятно также, что при условии с = r:
ДВ = Р
(здесь р — статистическая оценка).
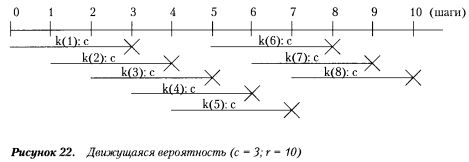
Построение графика движущейся вероятности будем проводить по следующей процедуре (см., например, рисунок для с = 3 и r = 10):
1) зафиксируем величину с на каком-то постоянном значении с = const < r;
2) посчитаем число «успехов» для первых с испытаний и с помощью полученного результата (k1) рассчитаем значение ДВ1 = k1/с; обозначим ДВ1 как p1;
3) сдвинем период с на один шаг вправо (в сторону увеличения количества испытаний) и аналогичным образом рассчитаем второе значение ДВ2 = р2 = к2 / с;
4) последовательно сдвигая один и тот же период вычислений с на один, рассчитаем значения p1, р2, р3, р4 и т.д, а затем проделаем эти вычисления для всего количества проведенных испытаний r;
5) полученные значения ДВ отложим на отдельном графике.
Отметим, что, показатель ДВ — это индикатор осцилляторного типа.
Движущаяся вероятность — это индикатор осцилляторного типа. Он показывает соотношение успешных и неудачных операций на некотором фиксированном, но постоянно «сдвигающимся» их числе.
Обратим внимание, что первое значение ДВ возникает на номере испытаний, которое равно периоду с. Иначе говоря, общее число значений ДВ будет меньше, чем количество испытаний на величину, равную (с - 1).
Так, для г = 10 и с = 3 получаем г - с + 1 = 8 каких-то произвольных значений ДВ, поскольку отсчет начинается с третьего шага (см. рисунок).
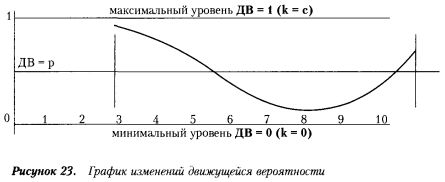
Высокие показатели ДВ говорят о превышении числа успехов как результата применения сигнала над количеством неудач. Это означает соответствующую выраженность движения графика эффективности вверх. Низкие значения ДВ, наоборот, отражают тенденцию к падению эффективности.
Если говорить более конкретно, то значения ДВ > 1/2 говорят о наличии преимущественного числа «успехов» в сравнении с «неудачами» за данный период наблюдения. При условии ДВ < 1/2 преимущество, наоборот, — у «неудачного» сценария. Иначе говоря, «чистый» результат (разница между числом «успехов и «неудач») будет прямо пропорционально зависеть от значения ДВ (см. рисунок).

Обратим внимание на обстоятельство, имеющее важное методическое значение.
Если рассмотреть динамику движения показателя ДВ, то существуют пять основных сценариев его изменения:
I. Возрастание ДВ от 0 до '/2.
II. Возрастание ДВ от 1/2 до 1.
III. Падение ДВ от 1 до '/2.
IV. Падение ДВ от 1/2 до 0.
V. «Зависание» ДВ на любом из уровней значения от 0 до 1.
Если соотнести динамику движения показателя ДВ с графиком изменений в дополнительном измерении (случайное блуждание), то получим следующие варианты соответствующих конфигураций:
• хотя возрастание значения ДВ от нулевого уровня до 1/2 сопровождается повышением «чистого результата», но он все равно остается отрицательным, это значит, что кривая случайного блуждания будет продолжать свое падение, хотя и замедляющимися темпами;
• последующее возрастание значения ДВ от '/ до 1 означает рост кривой случайного блуждания ускоряющимися темпами;
• хотя падение значения ДВ от 1 до 1/2 сопровождается снижением «чистого результата», но он все равно остается положительным, это значит, что кривая случайного блуждания будет продолжать свой рост, хотя и замедляющимися темпами;
• последующее снижение значения ДВ от '/ до 1 означает падение кривой случайного блуждания замедляющимися темпами;
• отсутствие выраженного направления изменения показателя ДВ («зависание») может сопровождаться различными вариантами изменения на графике случайного блуждания, но общим для всех них будет неизменность темпов роста или падения кривой.
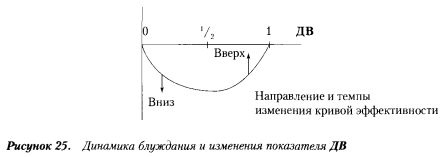
Эту зависимость направления и темпов изменения кривой случайного блуждания от направления и уровней изменения показателя ДВ можно представить на графике (см. рисунок).
Движущаяся изменчивость. Индикатор изменчивости (volatility) широко используется в техническом анализе применительно к традиционным пространствам, где она характеризует частоту и диапазон колебательных движений в поведении рынка.
Параметр движущейся изменчивости (ДИ) в дополнительном измерении отличается по своему содержанию от этого индикатора, хотя и вводится по аналогии с ним. Процедура его графического построения остается той же, что и у индикатора ДВ.
ДИ — это осциллятор, рассчитанный по доле v числа изменений и, которые фиксируются на протяжении некоторого постоянного количества испытаний (n = const):
v = u/n,
где v(max) = n -1 и v(min) = 0.
Показатель v описывает только частоту смены направления движения, которое наблюдается на графике эффективности на некотором заданном фиксированном отрезке испытаний (см. рисунок).
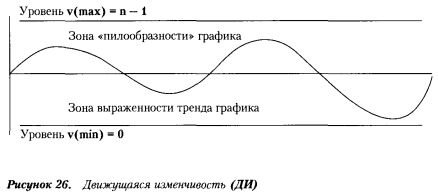
Движущаяся изменчивость — это индикатор осцилляторного типа. Он показывает число изменений направления, которое имело место на некотором фиксированном, но постоянно «сдвигающемся» числе операций.
Низкие значения изменчивости v говорят о наличии выраженного тренда в движении графика дополнительного измерения. Причем это может быть как возрастание, так и падение эффективности.
Высокая движущаяся изменчивость, «пилообразность» поведения этого графика, означает и «размытость» тренда. При максимальной изменчивости движение графика происходит в горизонтальном направлении.
Как и любые другие осцилляторы, ДВ и ДИ могут быть использованы, в частности, при анализе дивергенции, когда направление их изменения сравнивается с тенденцией движения на графике дополнительного измерения.
Кроме того, достижение экстремальных значений ДВ и ДИ в принципе можно рассматривать с точки зрения понятий «перевыкупленности — перераспроданности», но лишь в качестве отдаленных аналогов.
Определенные конфигурации и значения осцилляторов ДВ и ДИ могут быть использованы как при анализе дивергенции, так и явлений «перевыкупленности» и «перераспроданности».
Анализ показателей ДВ и ДИ может проводиться по крайней мере по двум направлениям.
Первое, предметом изучения избираются непосредственно значения этих показателей. Тогда при условии достижения неких предельных уровней возникает рациональная основа для соответствующих выводов.
Например, движение индексов ДВ и ДИ можно изучать с учетом существующих статистических закономерностей, присущих процессам с нормальным распределением, как это было только что рассмотрено применительно к характеристикам волнового движения. Скажем, исходя из того, что выход значений ДВ и ДИ за пределы трех стандартных отклонений — событие маловероятное, можно делать обоснованные вероятностные прогнозы, если фиксируется «пограничная» ситуация (т.е. индекс ДВ или ДИ достигает этого «маловероятного предела»).
Конечно, «инерция» может увести значения и на «запредельные» уровни, но вероятность такого события при повторениях ситуации невелика.
Второе направление — это построение обычных графиков изменения этих показателей. Тем самым создается еще один информационный массив, который используется для проведения всех описанных выше видов графического анализа.
Анализ показателей ДВ и ДИ может проводиться как по некоторым предельным уровням достижения, так и по конфигурациям графика изменений.
Практические выводы по результатам анализа в каждом отдельном случае должны быть рационально обоснованы действующими в дополнительном измерении закономерностями и соответствующими расчетами.
Особо подчеркнем, что речь идет лишь о предположительном прогнозе, который может и не оправдаться. Но при многократном повторении эксперимента в одних и тех же условиях чаще всего следует ожидать не маловероятных, а высоковероятных событий.
В конкретной серии реальных испытаний могут произойти любые принципиально возможные события.

Однако следует исходить из того, что повторы в одних и тех же исходных условиях будут неизбежно приводить не к маловероятным, а к наиболее вероятным событиям.
|

