|
Одним из важнейших расчетов для применения в рациональном управлении случаем являются оценки, полученные при решении классической задачи теории вероятностей о разорении в биномиальной модели.
Прикладное значение для нас имеют, прежде всего, выводы по таким показателям, как:
• вероятность достижения цели (выигрыша) или разорения;
• математическое ожидание выигрыша;
• средняя продолжительность игры до выигрыша или разорения.
Исходные условия данной задачи формулируются следующим образом:
• проводится серия игровых испытаний до «победы» или «разорения» при исходном капитале, составляющем z «условных» единиц;
• «победная» цель составляет w «условных» единиц (w - z является «чистым» выигрышем), после чего игра считается завершенной;
• первая игра (а также каждая последующая) с вероятностью р приводит к «прибыли», равной +1 «условной единице» капитала (тогда итоговая сумма становится z + 1), или с вероятностью q к «убытку», равному -1 (z -1);
• разорение определяется как «нулевое» состояние начального капитала z = 0.
Классическая задача о разорении формулируется при условии игры до «победы» (достижение цели w) или поражения (начальный капитал z = 0). При любом из этих исходов игра прекращается.
Иногда игровую биномиальную модель удобно интерпретировать как противостояние двух игроков (трейдер и рынок). Тогда для удовлетворения исходных условий необходимо исходить из того, что начальный капитал одного них (трейдера) составляет z, а другого (рынка) w - z.
Вероятность разорения/достижения. Приведем без вывода две общие формулы оценки вероятности разорения и достижения (выигрыша) для разных соотношений исходных вероятностей q и р.
1. Когда q не равно р (т. е. q < р или q > p ), верна формула
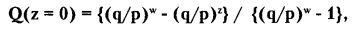
где р — вероятность «успеха», прибыль от которого в каждом отдельном испытании равна +1;
q — вероятность «неудачи», убыток от которой в каждом отдельном испытании равен -1.
Q(z = 0) — вероятность разорения, наступающего тогда, когда начальный капитал (z) становится равным 0; P(w) = 1 - Q(z = 0) — вероятность достижения цели: увеличение начального капитала (z) до величины w.
Пример 1. Игрок имеет 99 «условных единиц» начального капитала, а вероятности исходов в каждом испытании составляют соответственно: q = 0,55 и р = 0,45. Иначе говоря, вероятность «неудачи» несколько выше, чем «успеха».
Тем не менее, оказывается, что если в качестве цели поставить получение выигрыша лишь одной «условной единицы» капитала, то вероятность добиться «успеха» в этом составляет:
P(w = 100) = 1 - Q(z = 0) = 0,818.
Данный пример иллюстрирует общее правило:
• чем больше начальный капитал игрока, тем значительнее шансы выиграть малую сумму до того, как он разорится.
Даже при неблагоприятной вероятности «успеха» в каждом отдельном испытании шансы у игрока выиграть малую сумму, до того как он разорится, могут быть значительными. И они тем выше, чем больше начальный капитал.
В этой связи интерес представляет более детальная оценка изменения вероятности разорения в зависимости от постепенного увеличения ставки в неблагоприятных условиях (q > р).
Опуская математические выкладки, отметим, что при неизменности начального капитала постепенное увеличение ставки приводит к уменьшению вероятности разорения «обреченного» игрока. Соответственно, вероятность разорения для того, кому «успех» обеспечен по математическому ожиданию, увеличивается.
Это правило можно сформулировать так:
• в повторяющейся игре с постоянной ставкой вероятность
разорения игрока будет минимальной при выборе такой
ставки, которая была совместимой с суммой желаемого
выигрыша.
При неизменности начального капитала и повторяющейся игре с постоянной ставкой вероятность разорения будет минимальной при выборе такой ставки, которая была бы совместимой с суммой желаемого выигрыша.
Пример 2. Рассмотрим ту же «невыгодную» игровую ситуацию, при которой q = 0,55, р = 0,45. И пусть z = 90, a w = 100 «условных единиц».
Если при каждом испытании ставка будет равной одной «условной единице», то вероятность разорения, действительно, составит почти предельную величину:
Q(z = 0) = 0,866.
Но если увеличить ставку до максимально возможного значения (при заданных условиях оно равно w - z = 100 - 90 = 10), то столь неблагоприятный прогноз меняется кардинально. И хотя математическое ожидание выигрыша остается тем же, вероятность разорения составит всего лишь 0,210, а выигрыша — возрастет до 0,790.
Как видим, несмотря на неблагоприятное соотношения р и q, у «обреченного» игрока есть значительные шансы выйти победителем в какой-то из попыток.
Разумеется, эту победу можно сохранить лишь тогда, когда игрок имеет право тут же раскланяться и удалиться подальше от места игры.
2. По существу, близкие к этим результаты можно получить и для испытаний с «идеальной» монетой (q = p).
Правда, вышеприведенная формула оценки вероятности разорения здесь не годится. Выведена более простая:
Q(-z) = 1 - (z/w),
где (w - z) > 0 — «чистый» выигрыш.
Тогда вероятность такого исхода:
P(z) = 1 - Q(-z) = z/w.
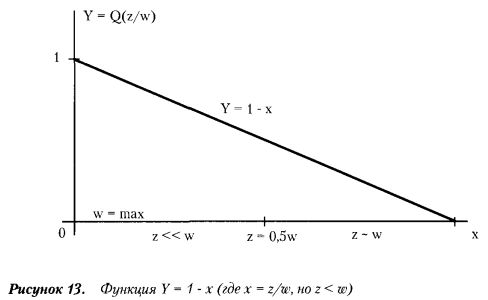
Если исследовать зависимость функции Q(z/w) от соотношения переменных z и w, то обнаруживается следующее (см. рисунок 13).
При некотором заданном постоянном значении z (z = const) вероятность разорения уменьшается по мере изменения величины w в сторону сближения с z. И вероятность разорения достигает минимальных значений, когда величины w и z становятся сравнимыми (z - w).
Это правило можно сформулировать таким образом:
• вероятность разорения в игре с постоянной ставкой становится минимальной при малом в сравнении с исходным капиталом z выигрыше как цели игры и максимально приближенной к «чистому» выигрышу (w - z) ставке.
При р = q вероятность разорения Q становится минимальной, а выигрыша Р — максимальной при двух условиях: 1) минимальная цель выигрыша; 2) максимальная ставка.
Пример 3. (это условия примера 2, но только для значения q = p). При ставке, равной 0,lz, получим, что:
w = z + 0,1z.
И тогда вероятность разорения
Q(-z) = 1 - (z/w) = 1 - z / (z + 0,lz) = 1 - 10 / 11 = 1 /11 = 0,09.
А вероятность выигрыша
P(w) = 0,1/1,1 = 0,91.
Приведем в этой связи некоторые расчеты для соотношений, с которыми реально имеет дело трейдер-индивидуал.
При этом обратим внимание на два существенных момента, касающихся условий игры:
1) ставка является аналогом стоп-ордера по прибыли (stop-profit) в каждом отдельном испытании (срабатывании «сигнала»);
2) исходный капитал z выполняет одновременно две функции: и стоп-ордера по убытку (stop-loss), и ордера «стоп-операция».
Пусть игрок имеет начальный капитал в $3000. Ставка (stop-profit) при каждой игре составляет $300. Это происходит при стоп-ордере в 30 базисных пунктов при операциях с британским фунтом стерлингов (GBP), скажем, против доллара США.
Тогда имеем условия: z = 3000 и w = 3300.
Но поскольку в качестве «условной единицы» служит величина $300, то в масштабе исчисления, использованного выше, это означает, что z = 10, а w = z + 0,1z = 11. И мы приходим к условиям и решениям примера 3, где: Q(-z) = 0,09 и P(w) = 0,91.
Как видим, при неблагоприятном соотношении р < q можно, управляя значениями w, z и размером ставки, добиться впечатляюще хороших пропорций Q(z) и P(w).
Математическое ожидание результата. Под математическим ожиданием выигрыша здесь понимается средний результат испытаний, который ожидается при повторении одной и той же игры.
В этой связи возникает вопрос о том, каково математическое ожидание результата, т.е. средний выигрыш в ходе продолжительного повторения игры, при условиях:
• неблагоприятного соотношения р < q;
• благоприятного соотношения Q(-z) < P(w).
Как следует из условий, конечный результат игры («победа» w или «поражение» z = 0) — это случайная переменная, которая принимает одно из двух значений:
• (w-z);
• (-z).
Тогда математическое ожидание выигрыша (Е) для любого, в том числе и равного, соотношения q и р:
Е = P(w) х (w - z) - Q(z = 0) x (-z) = w x P(w) - z.
А при q = p:
E = wx{1-Q(z = 0)}-z.
Если в эти формулы подставить значения Q(z = 0), то получим: Е(для q > р) < 0
и
E(q = р) = w X {1 - Q(z = 0)} - z = w X (z/w) - z = 0.
Если вернуться к предыдущим примерам, то в примере 1 математическое ожидание результата будет иметь отрицательную величину:
E(w = 100) = -17,2.
В примере 2 ожидания результата еще хуже:
E(w = 100) = -76,6.
Вместе с тем, знание этих расчетов позволяет выбирать «наименьшее зло». Таким образом, необходимо учитывать следующее важное правило:
• если игрок находится в неблагоприятных условиях р < q и ста вит задачу закончить игру либо после того, как выиграет сумму w, либо проиграет предельно допустимую сумму z, то никакие соотношения Q(-z) < P(w) не изменят негативного математического ожидания результата.
В биномиальных испытаниях негативное математическое ожидание выигрыша никак невозможно изменить в благоприятную сторону.
По выражению В. Феллера, это значит, что «небезобидная» игра (р < q) не может стать «безобидной» (р = q). Тем более ее нельзя сделать выигрышной (р > q).
Итак, никакие манипуляции с указанными переменными не позволяют рассчитывать на положительное значение математического ожидания. Хуже того, недостижимым является даже ноль.
Таким образом, порядок применения рационального способа управления случаем может быть следующим:
• для заданного соотношения р и q проводится расчет конкретного варианта соотношения величин w и z, при котором достигается максимальное математическое ожидание («наименьшее зло»).
При рациональном подходе следует для заданных р и q выбирать такие соотношения переменных w и z, которые обеспечивают наилучшее математическое ожидание.
Однако напомним, что речь идет о математическом ожидании результата при условии бесконечного числа испытаний.
В этой связи полезно рассмотреть оценки средней продолжительности игры, при которой, согласно теории вероятностей, могут быть достигнуты
заранее установленные цели. И данный параметр продолжительности также следует принимать во внимание в процессе управления.
Средняя продолжительность игры. Приведем без вывода основные формулы оценки средней продолжительности игры для разных соотношений р и q.
1. Для случая, когда q не равно р (р > q или р < q) и при размере исходного капитала z, а цели w (в каждой игре ставка составляет одну «условную единицу»), решение уравнения приводит к формуле:
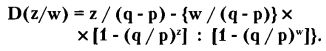
Вернемся к приведенному выше примеру 2, в котором существует положение «невыгодной» игры при q = 0,55 и р = 0,45 (z = 90, w = 100 «условных единиц»).
Мы уже видели, что если при каждом испытании ставка будет равной одной «условной единице», то вероятность разорения Q(z) = 0,866. Тогда вероятность выигрыша P(z) = 0,134.
По формуле расчета средней продолжительности игры получим, что ее математическое ожидание при этом составит:
D(z/w) = 767 испытаний.
Однако если увеличить ставку до максимальной, сделав ее равной 10 «условным единицам», то соответственно получим:
Q(z) = 0,210, a P(z) = 0,790.
И математическое ожидание продолжительности игры:
D(z/w) = 11 испытаний.
Соответствующее правило можно сформулировать так:
• чем меньше математическое ожидание продолжительности игры, тем вероятность выигрыша при «невыгодном» соотношении q > p становится все более благоприятной.
Чем меньше ожидаемая продолжительность «невыгодной» игры, тем лучше.
Этот расчет отвечает закону больших чисел: чем больше число испытаний, тем ближе будут результаты к математическому ожиданию вероятности «успеха».
2. Для q = p действительна другая формула, которая имеет вид:
D(z/w) = z x (w- z).
Сразу отметим, что средняя продолжительность игры оказывается значительно выше, чем это подсказывает нам «здравый смысл».
Так, если q = р, то при исходном капитале z = 90 условных единиц и желании игрока довести эту сумму до w = 100:
D(z = 90 / w = 100) = 90 х 10 = 900.
Заметим, что при ставке в 10 «условных единиц» вероятность «успеха» весьма высока:
P(z = 90 / w = 100) = 90 / 100 = 0,9.
Однако потребуется немало времени, чтобы получить тот или иной результат (разорение или «чистый» выигрыш в 10 единиц).
Даже если игрок ставит столь скромную задачу, как «окончательный выигрыш» всего одной «условной единицы» (w = z + 1), то продолжительность игры при капитале z = 90:
D(z = 90 / w = 91) = 90 х 1 = 90.
При этом вероятность «успеха» предельно благоприятна:
P(z = 90 / w = 91) = 90 / 91 = 0,99.
Обратим внимание на то обстоятельство, что, несмотря на высокую вероятность выигрыша, предстоит долгая борьба (в среднем 90 испытаний). И это для того, чтобы получить выигрыш, равный всего одной единице капитала.
Однако утешает то, что «условная единица» капитала может составить значительную сумму «живых» денег. Правда, тогда придется задействовать начальный капитал, который в 90 раз больше выигрыша.
Как видим, невозможно заранее задать наиболее «выгодный» путь: многое зависит от разных обстоятельств.
Вернемся к приведенному выше примеру 3, но в качестве одной «условной единицы» примем $300.
Тогда случайная величина D(w/z) с учетом новой «единицы» вычисляется по формуле:
D(w/z) = (z / 300) х (w - z) / 300.
Рассмотрим ожидаемую продолжительность игры в зависимости от того, какие цели ставит трейдер.
При желании выиграть $300, т.е. 10% от исходного капитала, получим следующие оценки:
• вероятность выигрыша
P(z = 3000 / w = 3300) = z / w = 3000 / 3300 = 10/11 = 0,91;
• продолжительность игры
D(w = 3300 / z = 3000) = (z / 300) х (w - z) / 300 = 10.
Сравним этот результат с другими условиями.
Пример 4. Если целью ставится увеличить капитал на 20% при той же ставке $300 в каждой игре:
• вероятность выигрыша
P(z = 3000 / w = 3600) = 10/12 = 0,83;
• продолжительность игры
D(w = 3600 / z = 3000) = 20.
Пример 5. Для двукратного «обогащения» при тех же условиях:
• вероятность выигрыша
P(z = 3000 / w = 6000) = z / w = 0,5;
• продолжительность игры
D(w = 6000 / z = 3000) = 200.
Таким образом, приведенные расчеты вновь подтверждают полученные уже ранее оценки: чем более масштабными являются цели, тем менее вероятным становится их достижение.
При этом продолжительность игры возрастает быстрее, чем интуитивно предполагается. В приведенном примере видно, что увеличение размера цели от 20 до 100% (в пять раз) увеличивает среднюю продолжительность игры с 20 до 200 испытаний (в десять раз).
Увеличение цели по прибыли при прочих равных условиях ведет к снижению вероятности выигрыша и непропорционально большому возрастанию продолжительности игры.
Итак, важный практический вывод:
• высокая вероятность «успеха» еще не означает легкость его достижения.

Тем не менее, знание всех перечисленных выше правил позволяет более грамотно и рационально подходить к принятию решений в области постановки стоп-ордеров.
|

