|
Это уже другая сторона проявления «воли случая», в которой интерес представляет не только то, насколько «успешной» была серия испытаний, но и каков путь, т.е. конфигурация движения к данному результату.
Ниже мы выделим основные закономерности, которые характеризуют наиболее существенные особенности конфигураций, возникающих в дополнительном измерении как пространстве случайных событий.
Если вновь вернуться к испытаниям с «идеальной» монетой, то их можно проводить по двум схемам:
1) путем повторения одинаковых серий (за счет изменения N при постоянном r); тогда мы убедимся в справедливости закона больших чисел: с ростом N разница между экспериментально получаемым значением k и k(ср), рассчитанным по теоретической модели, будет стремиться к нулю;
2) за счет увеличения продолжительности серии r при неизменности ее номера N, который останется равным 1.
Работу трейдера с определенным сигналом можно описать любой из этих схем. Но закономерные конфигурации удобнее изучать при фиксированном N.
Закон повторного логарифма: «беспредел». Вспомним, что закон больших чисел, справедливый для бесконечного значения N, по существу, говорит о невероятности отклонения экспериментально наблюдаемого числа к от математического ожидания этой величины. Но этот закон не утверждает, что число «успехов» к обязано оставаться близким к нему в каждой конкретной серии испытаний, т.е. при каком-то определенном N.
А что же там происходит? Об этом говорит закон повторного логарифма. Существо этого закона в том, что в ходе отдельно взятой серии испытаний, сколь бы продолжительной она ни была, могут происходить даже самые маловероятные события.
Для дальнейших пояснений удобно вместо переменной к (число «успехов») ввести так называемое «нормированное число успехов»:
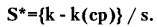
Далее, опуская математические выкладки, отметим два главных положения данного закона.
Первое. Хотя умеренные значения S более вероятны, однако максимум этой величины (т.е. отклонение числа успехов от математического ожидания) будет медленно возрастать. Тем самым, появляется принципиальная возможность для возникновения сколь угодно больших отклонений. Это своего рода «беспредел» в случайном поведении.
В достаточно длинном ряду испытаний существует возможность сколь угодно большого отклонения от математического ожидания.
Разумеется, здесь нет противоречия закону больших чисел, поскольку равновесие должно естественным образом восстанавливаться, в частности, при бесконечном увеличении числа серий (N) испытаний.
Второе. Практически наверняка последовательность максимумов таких отклонений будет определяться по формуле:
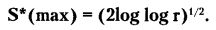
Именно в этом положении и заключено основное содержание закона повторного логарифма.
На основании этого закона принято делать вывод о том, что игрок, действующий в рамках модели «идеальной» монеты, может быть уверенным в одном: рано или поздно его выигрыш станет положительным.
Однако не следует забывать, что у этого закона есть и оборотная сторона: рано или поздно баланс «успехов» и «неудач» станет отрицательным.
Таким образом, вполне надежный путь добиться выигрыша существует только для игрока, располагающего неограниченным капиталом. Для этого достаточно терпеливо выждать момент, когда, согласно закону повторного логарифма, обязательно наступит «успех», после чего, издав победный клич, можно прекратить игру.
К сожалению, для игрока, который ограничен в средствах, далеко не всегда доступна такая нечаянная радость: может быть уже слишком поздно.
Как замечает В. Феллер, игроку с реально ограниченными ресурсами не остается ничего, кроме как воспользоваться своим правом закончить игру в благоприятный для него момент. Тогда ожидаемый результат игры не может быть оценен с помощью предельных теорем и нормального приближения, не дающих твердой надежды на благоприятный прогноз.
Точнее говоря, тогда вообще трудно рассчитать, какими могут быть результаты.
Если игрок имеет право прекратить игру в благоприятный для него момент, то результат не может быть оценен с помощью предельных теорем и нормального приближения. Возможны разные варианты.
Практическое значение закона повторного логарифма в том, что при каких-то условиях у игрока с «обычными» финансовыми ресурсами существует шанс «обойти» вердикт вероятностных расчетов, обрекающий на результат, который усреднен с точки зрения статистики.
Как выше отмечалось, оборотная сторона этого закона в том, что наряду с выигрышем равным образом существует и возможность полной потери исходного капитала.
Если представить игру как противоборство «трейдера», с одной стороны, и «рынка», с другой, то возникает явное «неравноправие». Ведь игрок-рынок имеет неограниченный капитал, а финансовые ресурсы игрока-трейдера очень и очень далеки от бесконечности.
Но, как говорится, еще не все потеряно. Чтобы убедиться в этом, обратимся к некоторым интересным формам проявления закона повторного логарифма.
Первая теорема (закон) арксинуса: «инерция тренда». Определенные надежды дает углубленный анализ конфигурации случайных движений, позволяющий получить более детальное представление о конкретных формах и периодичности распределения исходов.
Рассмотрим биномиальные испытания, продолжительность которых r.
Оказывается, что, например, в модели с «идеальной» монетой даже бесконечный рост r может не привести к равновесию числа «успехов» и «неудач».
Не обладая предварительными знаниями в этой области, трудно себе представить, что по мере возрастания величины r такое событие, как «равномерное распределение исходов», становится исключительно маловероятным.
В этом, собственно говоря, и заключено содержание первой теоремы (или закона) арксинуса.
Рассмотрим ее более детально.
Если представить результаты испытаний в виде кривой случайного блуждания в пространственно-временном измерении (допустим, верхняя половина — область «успеха», а нижняя — «неудач»), то более строгая с научной точки зрения формулировка звучит следующим образом: при фиксированной величине времени t (0 < t < 1) и числе испытаний (г), стремящемся к бесконечности, вероятность Р(k > r/2) того, что доля времени (k/r = t), которую точка блуждания проведет в верхней («успешной») половине графика, будет меньше t, и стремится к числу, определяемому по формуле:
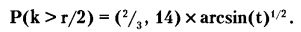
Выделим, в первую очередь, следующие три положения, вытекающие из данной теоремы, которые важны в практическом плане:
• наименее вероятным является событие: «доля времени, которую точка блуждания проведет на какой-то одной стороне (положительной или отрицательной), будет равна половине всего времени испытаний»;
• наоборот, верным является то, что наибольшую вероятность имеет событие: «будут иметь место крайние значения, т.е. при к, стремящемся к r или 0»;
• чем более продолжительными будут испытания, тем необратимее станет преимущество одного исхода над другим.
Согласно первому закону арксинуса, для серии испытаний r с «идеальной» монетой достижение баланса числа «успехов» и «неудач» — событие крайне маловероятное. Наиболее вероятный исход заключается в преимуществе какой-то одной стороны. И чем выше значение r, тем это преимущество может становиться все более устойчивым.
Парадоксальность первого закона арксинуса по праву считается удивительной. Проиллюстрируем это на примере 20 испытаний, вновь воспользовавшись аналогией «противостояние трейдер — рынок».
Как мы видели, согласно рассматриваемому закону, наиболее вероятным сценарием развития этого «противостояния» будет то, что в результате конкретной серии испытаний какая-то одна из сторон окажется «везунком», а другая — «неудачником».
Если сделать более точные расчеты, то вероятность для «неудачника» добиться хотя бы «ничьей» ничтожна: 0,06. Это означает, в частности, что почти определенно (вероятность 0,94) по результатам 20 бросков должен определиться победитель в данной серии. И чем больше число испытаний, тем эта вероятность выше.
Можно рассчитать и другие варианты.
Например, с вероятностью 0,35 в течение всего периода испытаний «неудачник» (или менее удачливый игрок) никогда не будет в выигрыше. А если и выиграет, то с вероятностью 0,54 не более одного раза.
В этом смысле можно говорить о том, что данный закон устанавливает неизбежное возникновение тренда в результатах испытаний.
Эти результаты вполне приложимы и к событиям в дополнительном измерении.
Согласно первому закону арксинуса, показатели эффективности в дополнительном измерении будет изменяться по некоторому тренду.
Народное наблюдение по поводу того, что кто-то «бился, колотился, а ничего не добился», — это, в известном смысле, иллюстрация первой теоремы арксинуса, с точки зрения «неудачника». Естественно, для «везунка» все видится иначе: «Иной Ивашка живет без промашки».
Таким образом, данная теорема позволяет, так сказать, воочию увидеть, в каком конкретном виде проявляет себя та или иная предрасположенность игрока, действующего в пространстве случайных событий.
Вопрос, который возникает в этой связи: как долго такой тренд «удачливости» (или «неудачливости») может продолжаться?
Для рассмотрения этого вопроса необходимо представить механизм возникновения тренда «удачливости» (или «неудачливости») в пространстве случайных событий.
В этих целях мы в следующем разделе обратимся к такому понятию, как инерция.
Теоремы о возвращении в начало координат: волна. Оценки возможной продолжительности тренда дают существующие теоремы о возвращении в начало координат. Они рассматривают смену времени «удачливости» периодом «невезучести» (и наоборот), что на графике движения выражается возвращением точки блуждания на «нулевую отметку».
О периодичности повторных возвращений можно судить по частоте «ничьих» (н). Поскольку, как мы знаем, r должно быть четным числом, то удобнее было бы обозначать общее число испытаний как 2r (r = 2r, где r — это целое положительное число, не равное нулю: 1, 2, 3 и т.д.).
Здравый смысл подсказывает, что чем больше испытаний, тем больше должно быть возвращений в начало координат, т.е. «ничьих» (н).
Это верно. Но зависимость здесь не является прямо пропорциональной. И на этот счет у В. Феллера приводится доказательства двух важных теорем.
Теорема 1. Основной является формула вероятности Р(н/2r) того, что точка вернется в начало координат н раз в течение периода испытаний 2r:
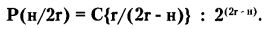
Можно рассчитать, что для всех испытаний, продолжительностью 2г, справедливо неравенство:
Р(н = 0) = Р(н = 1) > Р(н = 2) >... > Р(н = 2r).
Если его проанализировать, можно сделать следующие выводы.
1. Р(н = 0) = Р(н = 1) означает, что наиболее вероятным исходом будет полное отсутствие (н = 0) либо только одно (н = 1) возвращение в начало координат.
2. Р(н = 1) > Р(н = 2) >... > Р(н = 2r) означает, что одно возвращение более вероятно, чем два (н = 2). Но, в свою очередь, это событие более вероятно, чем три возвращения и т.д.
Повышенная вероятность меньшего числа возвращений объясняется тем, что если уж точка отклонилась от «нулевого уровня», то ей труднее вернуться обратно в начало координат, а тем более на противоположную сторону графика.
Таким образом, наиболее вероятными конфигурациями случайного блуждания являются тренд и полуволна (см. рисунок).
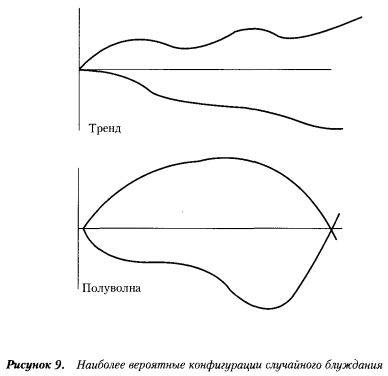
Согласно первой теореме о возвращении, наиболее вероятными конфигурациями при случайном блуждании являются тренд и полуволна.
Как видим, эти результаты полностью согласуются с первой теоремой арксинуса.
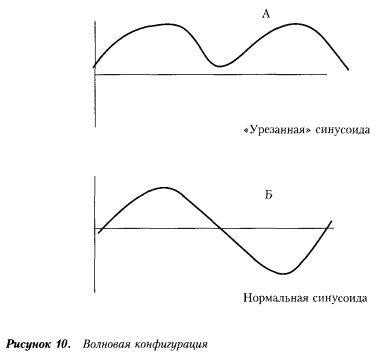
Очевидно, что точку завершения «полуволновой» конфигурации можно рассматривать как начало координат для последующего развития событий. Тогда следующая полуволна (см. рисунок) приведет к волне вида «урезанной» синусоиды (А) или ее нормального варианта (Б).
Теорема 2. Это конкретная оценка вероятностей, которые составляют содержание теоремы 1.
Речь идет о вероятности события, определенного как «не более чем некоторое заданное число возвращений в начало координат».
Как раз об этом и говорит теорема 2. В более строгой формулировке она звучит так: для некоторого фиксированного числа j > 0 вероятность того, что в серии испытаний от 0 до 2r точка блуждания вернется в начало координат не более j x (2r)0,5 раз (при возрастании 2r до бесконечности), стремится к следующей величине:
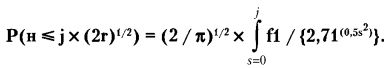
Мы не будем анализировать эту функцию, а лишь подчеркнем, что вероятность пересечения «нулевой отметки» будет возрастать пропорционально не 2r, а квадратному корню из этой величины (2r1/2).
Эта формула означает, что и длина волны будет также возрастать по мере увеличения числа испытаний.
Вторая теорема о возвращении показывает, что длина волны при возвращении точки случайного блуждания в начало координат будет возрастать пропорционально корню квадратному из числа испытаний (2r1/2), где 2r — длина данной серии.
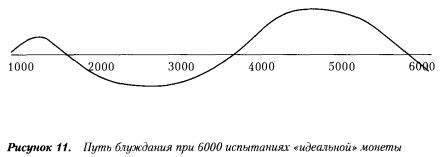
В качестве примера у В. Феллера приведены результаты серий из 6000 испытаний. При этом зафиксировано, что длина первой волны приблизительно 1000, второй — 2000 и третьей — 3000 шагов (см. рисунок).
По таблице нормальной функции распределения можно найти, что вероятность того, что произойдет не более 0,6745 х (2r)0,5 возвращений в ноль, близка к 0,5.
Тогда можно посчитать, что, например, для 10 000 испытаний с вероятностью 0,5 произойдет не более 68 «ничьих». Учитывая, что только половина приведет к смене лидерства (поскольку вероятность 0,5), средняя «длина волны» между последовательными изменениями лидерства составит примерно 300 шагов (в какой-то конкретной серии испытаний эта цифра, естественно, может быть иной).
Теоремы о возвращении точки блуждания в начало координат доказывают, что существуют два наиболее вероятных сценария развития событий при случайном блуждании. Один из них — ни одного возвращения. Другой сценарий, который является столь же вероятным, — это возникновение волновой конфигурации движения.
В этой связи возникает еще один вопрос: о расположении максимумов. Представление об этом позволит формулировать ожидания, обоснованными соответствующими вероятностными оценками.
Второй закон арксинуса: положение максимумов. Вспомним две совершенно противоречивые народные мудрости: «новичкам везет» и «первый блин — комом». Оказывается, что народ по-своему сформулировал вторую теорему арксинуса.
Оставляя за рамками нашего рассмотрения сложные расчеты, отметим только, что, согласно этому закону арксинуса, существует сильная тенденция к расположению максимумов вблизи начальной или конечной точек пути блуждания.
Однако народ это подметил гораздо раньше ученых мужей и отразил в своих мудрых поговорках.
Сценарий «первого блина» выражен в «законе бутерброда» (он же «закон подлости»). Слышится он и в поговорке: «Что ни начну, все неудача».
С другой стороны, очевидно, что именно данный закон послужил основой и для такого народного наблюдения: «новичкам везет», «и неладно, да удачливо», «за что ни возьмется, все ему удается».
Правда, так получается не у всех, а только у самых удачливых игроков. Иначе говоря, «везет тем, кого случай везет». А всем остальным новичкам гарантирован «первый блин комом».
Впрочем, всегда есть место для надежд на то, что со временем все образуется.
Второй закон арксинуса говорит о том, что одним новичкам «непременно повезет». Зато у других «первый блин» обязательно будет «комом».

Безусловно, в каждой отдельной серии испытаний конфигурация волны может быть различной, но тренды и волны следует воспринимать как наиболее вероятное развитие событий.
|

