Нейронные сети с прямой связью

Искусственная нейронная сеть построена из нейронов, связанных друг с другом. Даже если работа нейронной сети имитируется на компьютере, лучше представлять ее себе не как программу, а как электронную схему. Мы будем рассматривать два вида нейронных сетей: статические, которые также часто называют сетями с прямой связью (feed-forward), и динамические, или рекуррентные сети. В этом разделе мы займемся статическими сетями. Сети других видов будут кратко рассмотрены позднее.

Нейронные сети с прямой связью состоят из статических нейронов, так что сигнал на выходе сети появляется в тот же момент, когда подаются сигналы на вход. Организация (топология) сети может быть различной Если не все составляющие ее нейроны являются выходными, говорят, что сеть содержит скрытые нейроны. Наиболее общий тип архитектуры сети получается в случае, когда все нейроны связаны друг с другом (но без обратных связей). В конкретных задачах нейроны обычно бывают сгруппированы в слои. На рис. 1.3 показана типовая схема нейронной сети с прямой связью с одним скрытым слоем.

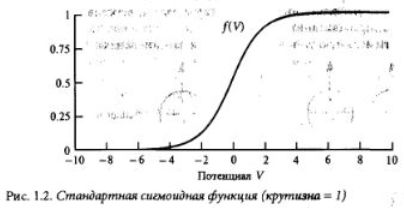
Интересно отметить, что, согласно теоретическим результатам 179], [118], нейронные сети с прямой связью и с сигмоидными функциями являются универсальным средством для приближения (аппроксимации) функций. Говоря точнее, любую вещественнозначную функцию нескольких переменных на компактной области определенно можно сколь угодно точно приблизить с помощью трехслойной сети. При этом, правда, мы не знаем ни размеров сети, которая для этого потребуется, ни значений весов. Более того, из доказательства этих результатов видно, что число скрытых элементов неограничен но возрастает при увеличении точности приближения. Сети с прямой связью, действительно, могут служить универсальным средством для аппроксимации, но нет никакого правила, позволяющего найти оптимальную топологию сети дли данной задачи.

Таким образом, задача построения нейронной сети является нетривиальной. Вопросы о том, сколько нужно взять скрытых слоев, сколько элементов в каждом из них, сколько связей и какие обучающие параметры, в имеющейся литературе, как правило, трактуются облегченно. Предлагаемая обычно процедура состоит в переборе различных архитектур с целью найти "наилучшую" или хотя бы удовлетворительную модель. Такая концепция представляется весьма ограниченной.

В литературе можно найти многочисленные «правила большого пальца» для определения числа скрытых узлов или количества весовых коэффициентов. В качестве рецептов могут предлагаться: среднее арифметическое числа входов и выходов, половина числа входов или удвоенный квадратный корень из произведения входов и выходов. Такие предложения математически необоснованны, и исследования в этой области ведутся очень активно.

Каждый узел многослойной сети проектирует свой входной вектор на вектор весов посредством скалярного произведения. Таким образом, в простейшем случае сети с одним скрытым слоем вектор входного сигнала проектируется на вектор весов каждого из нейронов скрытого слон. В результате мы получаем иное представление входного сигнала. После этого результаты проекций подвергаются нелинейным преобразованиям. Их цель — усилить те характеристике, за которые отвечает соответствующий узел. Компоненты вектора весов каждого узла подобраны так, чтобы выделить определенные свойства сигнала. Посредством нелинейного преобразования способность узла улавливать эти свойства увеличивается. Число характеристик, которые нужно уловить, чтобы осуществить правильную конструкцию сети, зависит от исходной задачи.

Выбор вариантов схемы сети может быть сужен также за счет априорных знаний о задаче. Так, Ле Куном [I75] была разработана сеть с "распределенными весами" для цифрового распознавания рукописного текста (где разные области входного изображения накрывались одинаковыми масками, извлекающими нужные характеристики).

Итак, мы описали, каким образом сеть с прямой связью осуществляет преобразование сигнала посредством весов, приписанных соединениям. Но как правильно выбрать значения этих весов? Этот момент обычно называют "обучением" или "тренировкой сети". Мы займемся им в следующем разделе.

ОБУЧЕНИЕ

На этапе обучения происходит вычисление синаптических коэффициентов в процессе решения нейронной сетью задач (классификации, предсказания временных рядов и др.), в которых нужный ответ определяется не по правилам, а с помощью примеров, сгруппированных в обучающие множества. Такое множество состоит из ряда примеров с указанным для каждого из них значением выходного параметра, которое было бы желательно получить. Действия, которые при этом происходят, можно назвать контролируемым обучением: "учитель" подает на вход сети вектор исходных данных, а на выходной узел сообщает желаемое значение результата вычислений. Контролируемое обучение нейронной сети можно рассматривать как решение оптимизационной задачи. Ее целью является минимизация функции ошибок, или невязки, Е на данном множестве примеров путем выбора значений весов W. Суть задачи оптимизации станет яснее, если представить себе график невязки, рассматриваемой как функция весов (эта функция определена в многомерном пространстве весов, где каждому весовому коэффициенту соответствует своя размерность). Из-за нелинейностей функций активации полученная поверхность в общем случае будет очень сложной: наряду с плоскими участками на ней будут локальные минимумы, седловые точки, овраги.

Содержание

Далее

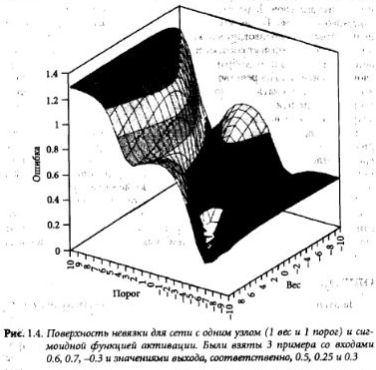
На рис. 1.4 видно, что даже простая сеть может реализовывать сложный нелинейный процесс.